
科目: 来源: 题型:
【题目】在平面直角坐标系中,等边![]()
![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() ,点
,点![]() ,点
,点![]() 在第一象限.
在第一象限.
(1)若抛物线![]() 经过点
经过点![]() 、
、![]() 、
、![]() ,求抛物线
,求抛物线![]() 的表达式.
的表达式.
(2)点![]() 是平面内一点,以点
是平面内一点,以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,现将抛物线
为顶点的四边形是平行四边形,现将抛物线![]() 平移得到抛物线
平移得到抛物线![]() ,若抛物线
,若抛物线![]() 经过
经过![]() 、
、![]() 两点,求抛物线
两点,求抛物线![]() 的表达式.
的表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”,为了选拔“阳光大课堂”领操员校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
若任意选择一名领操员的可能性相同
(1)任意选取一名领操员,选到成绩最低领操员的概率是_________.
(2)已知获得10分的选手中,七、八、九年级分别有1人,2人,1人,学校准备从中随机选取两人领操,求恰好选到八年级两名领操员的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】为提高饮水质量,越来越多的居民选择家用净水器,光明商场计划从生产厂家购进甲、乙两种型号的家用净水器,甲型号净水器进价为160元/台,乙型号净水器进价为280元/台,经过协商沟通,生产厂家拿出了两种优惠方案:第一种优惠方案:甲、乙两种型号净水器均按进价的8折收费;第二种优惠方案:甲型号净水器按原价收费,乙型号净水器的进货量超过10台后超过的部分按进价的6折收费.
光明商场只能选择一种优惠方案,已知光明商场计划购进甲型号净水器数量是乙型号净水器数量的1.5倍,设光明商场购进乙型号净水器![]() 台,选择第一种优惠方案所需费用为片
台,选择第一种优惠方案所需费用为片![]() 元,选择第二种优惠方案所需费用为
元,选择第二种优惠方案所需费用为![]() 元.
元.
(1)分别求出![]() 、
、![]() 与
与![]() 的关系式:
的关系式:
(2)光明商场计划购进乙型号净水器40台,请你为光明商场选择合适的优惠方案,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】九(1)班同学为了解某小区家庭月均用水情况(单位:吨),随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
25 | 2 | 0.04 |
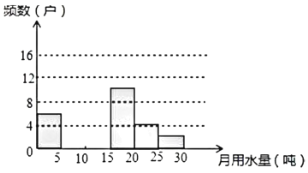
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区有1000户家庭,根据调查数据估计,该小区月均有水量超过20吨的家庭大约有多少户?
查看答案和解析>>
科目: 来源: 题型:
【题目】某汽车经销商为了能更好的了解某季度纯电动汽车的续航能力,现分两次不重复的各抽取了10台纯电动车进行了续航里程的测试.并将测试的情况进行整理、描述和分析(续航里程用x表示,共分成四组:(A)100≤x<200,(B)200≤x<300,(C)300≤x<400,(D)x≥400,单位:km).下面给出了部分信息:
第一次抽取10台车的续航里程在C组中的数据是:380,310,300,310.
第二次抽取10台车的续航里程是:220,301,175,310,400,310,385,430,234,455.
第一次测试的续航里程扇形统计图如图
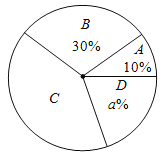
两次测试的续航里程统计表
第一次 | 第二次 | |
平均里程 | 321.4 | b |
中位数 | c | 310 |
众数 | 310 | 310 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中a、b、c的值,a= ,b= ,c .
(2)根据以上数据,你认为这两次测试中的哪一次的纯电动汽车续航能力更强?请说明理由(一条理由即可).
(3)若经销商这一季度共购进1600台纯电动汽车,结合这两次测试,估计这一季度续航能力较强(x≥380)的纯电动汽车有多少辆?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为1,对角线AC、BD交于点O,E是BC延长线上一点,且AC=EC,连接AE交BD于点P.
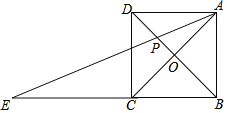
(1)求∠DAE的度数;
(2)求BP的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,∠CAF=2∠B.
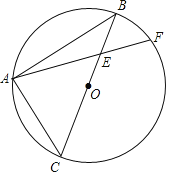
(1)求证:AE=AC;
(2)若⊙O的半径为4,E是OB的中点,求EF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A、B城往C、D两乡运肥料的平均费用如下表. 现C乡需要肥料240吨,D乡需要肥料260吨.
A城(出) | B城(出) | |
C乡(人) | 20元/吨 | 15元/吨 |
D乡(人) | 25元/吨 | 30元/吨 |
(1)A城和B城各多少吨肥料?
(2)设从B城运往D乡肥料x吨,总运费为y元,求y与x之间的函数关系,并写出自变量x的取值范围;
(3)由于更换车型,使B城运往D乡的运费每吨减少a元(a>0),其余路线运费不变,若C、D两乡的总运费最小值不少于10040元,求a的最大整数值.
查看答案和解析>>
科目: 来源: 题型:
【题目】哈市红十字预计在2019年儿童节前为郊区某小学发放学习用品,联系某工厂加工学习用品.机器每小时加工产品的数量比手工每小时加工产品的数量的2倍多9件,若加工1800件这样的产品,机器加工所用的时间是手工加工所用时间的![]() 倍.
倍.
(1)求手工每小时加工产品的数量;
(2)经过调查该小学的小学生的总数不超过1332名,每名小学生分发两个学习用品,工厂领导打算在两天内(48小时)完成任务,打算以机器加工为主,同时人工也参与加工(人工与机器加工不能同时进行),为了保证按时完成加工任务,人工至少要加工多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com