
科目: 来源: 题型:
【题目】疫情爆发,某企业准备转型生产口罩.该企业在市场上物色到两种生产![]() 口罩的设备,若采购2台
口罩的设备,若采购2台![]() 型设备,5台
型设备,5台![]() 型设备则共需要430万元;若采购5台
型设备则共需要430万元;若采购5台![]() 型设备,2台
型设备,2台![]() 型设备则共需要550万元.已知
型设备则共需要550万元.已知![]() 型设备每台每天可以生产19万片
型设备每台每天可以生产19万片![]() 口罩;
口罩;![]() 型设备每台每天可以生产8万片
型设备每台每天可以生产8万片![]() 口罩.
口罩.
(1)求![]() 、
、![]() 两型设备的采购单价分别是多少万元/台?
两型设备的采购单价分别是多少万元/台?
(2)该企业准备采购![]() 、
、![]() 两型设备共10台,但能用来采购设备的资金不超过700万元,那么如何安排采购方案,用这些设备每天生产的
两型设备共10台,但能用来采购设备的资金不超过700万元,那么如何安排采购方案,用这些设备每天生产的![]() 口罩最多?每天最多可生产多少万片
口罩最多?每天最多可生产多少万片![]() 口罩?
口罩?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直径![]() 把圆
把圆![]() 分为两个半圆,一个半圆弧上有一定点
分为两个半圆,一个半圆弧上有一定点![]() ,另一半圆弧上有一动点
,另一半圆弧上有一动点![]() .过
.过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
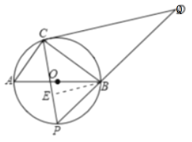
(1)求证:![]()
(2)若![]() ,
,![]()
①当点![]() 运动到半圆弧
运动到半圆弧![]() 中点时,求
中点时,求![]() 边
边![]() 上的高;
上的高;
②当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积最大?并求这个最大面积
的面积最大?并求这个最大面积![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,对称轴为直线
,对称轴为直线![]() ,顶点为
,顶点为![]() .
.
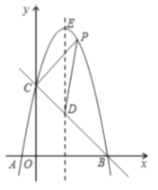
(1)求该二次函数的解析式;
(2)经过![]() 、
、![]() 两点的直线交抛物线的对称轴于点
两点的直线交抛物线的对称轴于点![]() ,点
,点![]() 为直线
为直线![]() 上方抛物线上的一动点,当点
上方抛物线上的一动点,当点![]() 在什么位置时,
在什么位置时,![]() 的面积最大?并求此时点
的面积最大?并求此时点![]() 的坐标及
的坐标及![]() 的最大面积;
的最大面积;
(3)如图,平移抛物线,使抛物线的顶点![]() 在射线
在射线![]() 上移动,点
上移动,点![]() 平移后的对应点为
平移后的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 、
、![]() ,
,![]() 是否能为等腰三角形?若能,请求出所有符合条件的点
是否能为等腰三角形?若能,请求出所有符合条件的点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
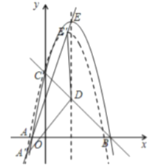
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,将线段
轴的正半轴上,将线段![]() 绕点
绕点![]() 顺时针旋转90°得到
顺时针旋转90°得到![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() .
.
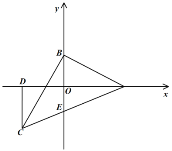
(1)当点![]() 在第三象限时,求实数
在第三象限时,求实数![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,设![]() ,当
,当![]() 取得最大值时,求图象经过
取得最大值时,求图象经过![]() 两点的二次函数
两点的二次函数![]() 的解析式;
的解析式;
(3)在(2)的条件下,将直线![]() 向上平移
向上平移![]() 个单位后与二次函数
个单位后与二次函数![]() 的图象交点的横坐标为
的图象交点的横坐标为![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 表示以
表示以![]() 为自变量的函数,则
为自变量的函数,则![]() 表示当
表示当![]() 时
时![]() 函数的值.例如,一次函数
函数的值.例如,一次函数![]() 记作
记作![]() ,当
,当![]() 时,函数值
时,函数值![]() .现给出新定义:对于函数
.现给出新定义:对于函数![]() ,若存在实数
,若存在实数![]() ,使得成立
,使得成立![]() ,则称点
,则称点![]() 是函数
是函数![]() 的“奇妙点”.
的“奇妙点”.
(1)求函数![]() 的“奇妙点”;
的“奇妙点”;
(2)当![]() 为何值时,函数
为何值时,函数![]() 存在“奇妙点”?
存在“奇妙点”?
(3)若二次函数![]() 有且只有一个“奇妙点”
有且只有一个“奇妙点”![]() ,其图象与
,其图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),
的左侧),![]() 是
是![]() 轴上一动点.当
轴上一动点.当![]() 的周长最短时,求点
的周长最短时,求点![]() 的坐标及
的坐标及![]() 的周长.
的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 的直径
的直径![]() ,点
,点![]() 为
为![]() 的延长线上一点,直线
的延长线上一点,直线![]() 切
切![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() 交
交![]() 于点
于点![]() ,连接
,连接 ![]() .
.
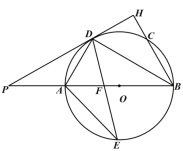
(1)求证:![]() 平分
平分![]() ;
;
(2)求![]() 的长;
的长;
(3)![]() 是
是![]() 上的一动点,
上的一动点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .是否存在点
.是否存在点![]() ,使得
,使得![]() ?如果存在,请证明你的结论,并求
?如果存在,请证明你的结论,并求![]() 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某电子产品销售公司专门销售某种品牌的电子产品.该公司给职工的工资由两部分组成:一是基本保障工资,二是销售奖励工资(销售奖励工资=销售每件产品的奖励金额×销售的件数).下表是小张、小李两位职工今年11月份的工资情况信息:
职工 | 小张 | 小李 |
月销售件数(件) | 200 | 180 |
月工资(元) | 5000 | 4700 |
(1)该公司职工的月基本保障工资和销售每件产品的奖励金额各是多少元?
(2)该公司职工小王计划今年12月份获得不少于6000元,那么小王12月份至少应销售多少件产品?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.

(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com