【题目】如图，在中，，是边上的中点，是边上任意一点，且．若点关于直线的对称点恰好落在的中位线上，则__________．

【题目】如图，已致点的坐标为，点在轴的正半轴上，且．过点作，交轴于点；过点作，交轴于点；过点作，交轴于点；……；按此规律进行下去，则点的坐标为（ ）

A.B.C.D.

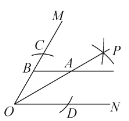
【题目】如图，已知，以点为圆心，适当长度为半径作弧，分别交边于点，分别以为圆心，大于的长为半径作弧，两弧在内交于点，作射线．若是上一点，过点作的平行线交于点，且，则直线与之间的距离是（ ）

A.B.C.3D.6

A.B.C.D.

分解因式：．观察知，显然时，原式，因此原式可分解为与另一个整式的积．令：，而，因等式两边同次幂的系数相等，则有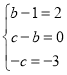：，得，从而

根据以上材料，理解并运用材料提供的方法，解答以下问题：

（1）若是多项式的因式，求的值并将多项式分解因式．

（2）若多项式含有因式及，求的值．

上，通过推动左侧活页门开关；图2是其俯视图简化示意图，已知轨道 ,两扇活页门的宽 ,点固定，当点在上左右运动时，与的长度不变(所有结果保留小数点后一位).

(1)若,求的长；

(2)当点从点向右运动60时，求点在此过程中运动的路径长.

（参考数据：sin50°≈0.77, cos50°≈0.64, tan50°≈1.19, π取3.14）

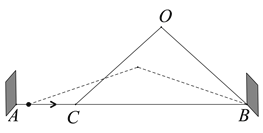
图1 图2

【题目】如图：在数轴上点表示数，点表示数，点表示数是最大的负整数，且满足．

（1）a=________，b=________，c=________．

（2）若将数轴折叠，使得点与点重合，则点与数________表示的点重合；

（3）点开始在数轴上运动，若点以每秒1个单位长度的速度向左运动，同时，点和点分别以每秒2个单位长度和3个单位长度的速度向右运动，假设秒钟过后，若点与点之间的距离表示为，点与点之间的距离表示为，则________，________．（用含的代数式表示）

（4）的值是否随着时间t的变化而改变?若变化，请说明理由；若不变，请求其值。

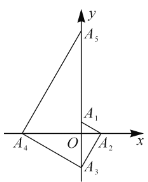
【题目】如图，所有正三角形的一边平行于轴，一顶点在轴上，从内到外，它们的边长依次为2，4，6，8，…，顶点依次用表示，其中与轴、底边与与、…均相距一个单位，则顶点的坐标是__________，的坐标是__________．

A.B.C.D.

【题目】如图，一艘船由港沿北偏东65°方向航行至港，然后再沿北偏西40°方向航行至港，港在港北偏东20°方向，则两港之间的距离为（　　）．

A.B.C.D.