
科目: 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
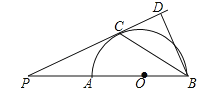
(1)∠PBC=∠CBD;
(2)![]() =ABBD.
=ABBD.
查看答案和解析>>
科目: 来源: 题型:
【题目】有大小两种货车,![]() 辆大货车与
辆大货车与![]() 辆小火车一次可以运货
辆小火车一次可以运货![]() 吨,
吨,![]() 辆大货车与
辆大货车与![]() 辆小货车一次可以运货
辆小货车一次可以运货![]() 吨.
吨.
(1)求![]() 辆大货车和
辆大货车和![]() 辆小货车一次可以分别运多少吨;
辆小货车一次可以分别运多少吨;
(2)现有![]() 吨货物需要运输,货运公司拟安排大小货车共
吨货物需要运输,货运公司拟安排大小货车共![]() 辆把全部货物一次运完.求至少需要安排几辆大货车?
辆把全部货物一次运完.求至少需要安排几辆大货车?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,线段AB=4,点C为线段AB上任意一点(与端点不重合),分别以AC、BC为边在AB的同侧作正方形ACDE和正方形CBGF,分别连接BF、EG交于点M,连接CM,设AC=x,S四边形ACME=y,则y与x的函数表达式为y=_____.
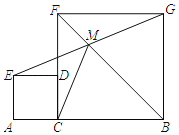
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以正六边形ABCDEF的中心O为原点建立平面直角坐标系,过点A作AP1⊥OB于点P1,再过P1作P1P2⊥OC于点P2,再过P2作P2P3⊥OD于点P3,依次进行……若正六边形的边长为1,则点P2019的横坐标为_____.
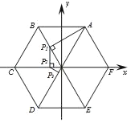
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=![]() x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点Q是线段OB上一动点,连接BC,点M在线段BC上,且使△BQM为直角三角形的同时△CQM为等腰三角形,则此时点Q的横坐标为( )
x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点Q是线段OB上一动点,连接BC,点M在线段BC上,且使△BQM为直角三角形的同时△CQM为等腰三角形,则此时点Q的横坐标为( )
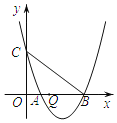
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A(﹣4,8)和点B(2,n)在抛物线y=ax2上.
(Ⅰ)求该抛物线的解析式和顶点坐标,并求出n的值;
(Ⅱ)求点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求此时点Q的坐标;
(Ⅲ)平移抛物线y=ax2,记平移后点A的对应点为A',点B的对应点为B',点C(﹣2,0)是x轴上的定点.
①当抛物线向左平移到某个位置时,A'C+CB'最短,求此时抛物线的解析式;
②D(﹣4,0)是x轴上的定点,当抛物线向左平移到某个位置时,四边形A'B'CD的周长最短,求此时抛物线的解析式(直接写出结果即可).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正方形OABC在平面直角坐标系中,点A,C分别在x轴,y轴的正半轴上,等腰直角三角形OEF的直角顶点O在原点,E,F分别在OA,OC上,且OA=4,OE=2.将△OEF绕点O逆时针旋转,得△OE1F1,点E,F旋转后的对应点为E1,F1.
(Ⅰ)①如图①,求E1F1的长;②如图②,连接CF1,AE1,求证△OAE1≌△OCF1;
(Ⅱ)将△OEF绕点O逆时针旋转一周,当OE1∥CF1时,求点E1的坐标(直接写出结果即可).

查看答案和解析>>
科目: 来源: 题型:
【题目】某水果批发市场规定,批发苹果不少于![]() 时,批发价为5元/
时,批发价为5元/![]() .小王携带现金4000元到这市场采购苹果,并以批发价买进.
.小王携带现金4000元到这市场采购苹果,并以批发价买进.
(Ⅰ)根据题意,填表:
购买数量 |
|
|
|
|
花费 |
|
| ||
剩余现金 |
|
|
(Ⅱ)设购买的苹果为![]() ,小王付款后还剩余现金
,小王付款后还剩余现金![]() 元.求
元.求![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)根据题意填空:若小王剩余现金为700元,则他购买__________![]() 的苹果.
的苹果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com