
科目: 来源: 题型:
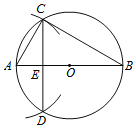
【题目】已知⊙O.如图,
(1)作⊙O的直径AB;
(2)以点A为圆心,AO长为半径画弧,交⊙O于C,D两点;
(3)连接CD交AB于点E,连接AC,BC.
根据以上作图过程及所作图形,有下面三个推断:
①CE=DE; ②BE=3AE; ③BC=2CE.
所有正确推断的序号是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,抛物线
,抛物线![]() 与
与![]() 轴从左到右的交点为
轴从左到右的交点为![]() ,
,![]() .
.
(1)若抛物线![]() 经过点
经过点![]() ,求抛物线
,求抛物线![]() 的解析式和顶点坐标;
的解析式和顶点坐标;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
①求点![]() 的坐标;
的坐标;
②若线段![]() 与抛物线
与抛物线![]() 有唯一公共点,直接写出正整数
有唯一公共点,直接写出正整数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一段铁路的示意图,![]() 段和
段和![]() 段都是高架桥,
段都是高架桥,![]() 段是隧道.已知
段是隧道.已知![]() ,
,![]() ,
,![]() ,在
,在![]() 段高架桥上有一盏吊灯,当火车驶过时,灯光可垂直照射到车身上,已知火车甲沿
段高架桥上有一盏吊灯,当火车驶过时,灯光可垂直照射到车身上,已知火车甲沿![]() 方向匀速行驶,当火车甲经过吊灯时,灯光照射到火车甲上的时间是
方向匀速行驶,当火车甲经过吊灯时,灯光照射到火车甲上的时间是![]() ,火车甲通过隧道的时间是
,火车甲通过隧道的时间是![]() ,如果从车尾经过点
,如果从车尾经过点![]() 时开始计时,设行驶的时间为
时开始计时,设行驶的时间为![]() ,车头与点
,车头与点![]() 的距离是
的距离是![]() .
.

(1)火车甲的速度和火车甲的长度
(2)求![]() 关于
关于![]() 的函数解析式(写出
的函数解析式(写出![]() 的取值范围),并求当
的取值范围),并求当![]() 为何值时,车头差
为何值时,车头差![]() 米到达
米到达![]() 点.
点.
(3)若长度相等的火车乙以相同的速度沿![]() 方向行驶,且火车甲乙不在隧道内会车(会车时两车均不在隧道内),火车甲先进隧道,当火车甲的车头到达
方向行驶,且火车甲乙不在隧道内会车(会车时两车均不在隧道内),火车甲先进隧道,当火车甲的车头到达![]() 点时,火车乙的车头能否到达
点时,火车乙的车头能否到达![]() 点?若能到达,至多驶过地点多少?若不能到达,至少距离
点?若能到达,至多驶过地点多少?若不能到达,至少距离![]() 点多少
点多少![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
【题目】把正整数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 排成如下的一个数表.
排成如下的一个数表.

(1)![]() 在第_____行,第______列;
在第_____行,第______列;
(2)第![]() 行第
行第![]() 列的数是_______(用含“
列的数是_______(用含“![]() ”的代数式表示)
”的代数式表示)
(3)嘉嘉和淇淇玩数学游戏,嘉嘉对淇淇说:“你从数表中挑一个数![]() ,按如图所示的程序计算,只要你告诉我所得的数在第几行,我就知道你挑的数在第几行.”你认为嘉嘉说得有道理吗?计算说明理由.
,按如图所示的程序计算,只要你告诉我所得的数在第几行,我就知道你挑的数在第几行.”你认为嘉嘉说得有道理吗?计算说明理由.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个
”中的每个![]() 内,填入
内,填入![]() ,
,![]() ,
,![]() ,
,![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若![]() ,请推算
,请推算![]() 内的符号;
内的符号;
(3)在“![]() ”的内填入符号后,使计算所得数最小,直接写出这个最小数.
”的内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,菱形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 的速度向点
的速度向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 支向点
支向点![]() 运动,当其中一个动点停止时另一个动点也随之停止,设运动时间为
运动,当其中一个动点停止时另一个动点也随之停止,设运动时间为![]() (单位:
(单位:![]() )(
)(![]() ),以点
),以点![]() 为圆心,
为圆心,![]() 长为半径的⊙M与射线
长为半径的⊙M与射线![]() 、线段
、线段![]() 分别交于点
分别交于点![]() 、
、![]() ,连接
,连接![]() .
.
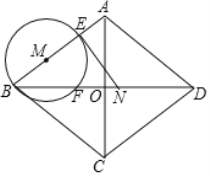
(1)求![]() 的长(用含有
的长(用含有![]() 的代数式表示),并求出
的代数式表示),并求出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,线段
为何值时,线段![]() 与⊙M相切?
与⊙M相切?
(3)若⊙M与线段![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】文具店有三种品牌的6个笔记本,价格是4,5,7(单位:元)三种,从中随机拿出一个本,已知![]() (一次拿到7元本)
(一次拿到7元本)![]() .
.
(1)求这6个本价格的众数.
(2)若琪琪已拿走一个7元本,嘉嘉准备从剩余5个本中随机拿一个本.
①所剩的5个本价格的中位数与原来6个本价格的中位数是否相同?并简要说明理由;
②嘉嘉先随机拿出一个本后不放回,之后又随机从剩余的本中拿一个本,用列表法求嘉嘉两次都拿到7元本的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() ,
,![]() .
.
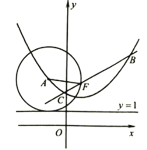
(1)求![]() 的值,并将抛物线解析式化成顶点式;
的值,并将抛物线解析式化成顶点式;
(2)已知点![]() ,点
,点![]() 为抛物线上一动点.求证:以
为抛物线上一动点.求证:以![]() 为圆心,
为圆心,![]() 为半径的圆与直线
为半径的圆与直线![]() 相切;
相切;
(3)在(2)的条件下,点![]() 为抛物线上一动点,作直线
为抛物线上一动点,作直线![]() ,与抛物线交于点
,与抛物线交于点![]() .当
.当![]() 时,请直接写出直线
时,请直接写出直线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com