
分析 利用对数的基本运算性质进行检验:(1)f(x1+x2)=lg(x1+x2)≠f(x1)f(x2)=lgx1•lgx2,
(2)f(x1•x2)=lgx1x2=lgx1+lgx2=f(x1)+f(x2),(3)f(x)=lgx在(0,+∞)单调递增,可得 $\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0
(4)(5)f($\frac{{x}_{1}+{x}_{2}}{2}$)=lg($\frac{{x}_{1}+{x}_{2}}{2}$),$\frac{f({x}_{1})+f({x}_{2})}{2}$=$\frac{lg{x}_{1}+lg{x}_{2}}{2}$,由基本不等式可得结果.
(6)利用函数的奇偶性判断即可.
解答 解:(1)f(x1+x2)=lg(x1+x2)≠f(x1)f(x2)=lgx1•lgx2
所以(1)不正确;
(2)f(x1•x2)=lgx1x2=lgx1+lgx2=f(x1)+f(x2)所以(2)正确;
(3)f(x)=lgx在(0,+∞)单调递增,则对任意的0<x1<x2,d都有f(x1)<f(x2)
即$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,所以(3)正确.
(4)f($\frac{{x}_{1}+{x}_{2}}{2}$)=lg($\frac{{x}_{1}+{x}_{2}}{2}$),$\frac{f({x}_{1})+f({x}_{2})}{2}$=$\frac{lg{x}_{1}+lg{x}_{2}}{2}$=$\frac{lg({x}_{1}{x}_{2})}{2}$
∵$\frac{{x}_{1}+{x}_{2}}{2}$≥$\sqrt{{x}_{1}{x}_{2}}$∴lg$\frac{{x}_{1}+{x}_{2}}{2}$≥lg$\sqrt{{x}_{1}{x}_{2}}$=$\frac{1}{2}$lg(x1x2),所以(4)不正确;(5)正确;
(6)f(x)=lgx函数不是偶函数,所以(6)不正确.
故答案为:(2)(3)(5).
点评 本题主要考查了对数的基本运算性质,对数函数单调 性的应用,基本不等式的应用,属于知识的简单综合应用.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:填空题
 如图,在正方形ABCD中,点E是DC的中点,点F是BC的一个三等分点,那么$\overrightarrow{EF}$=$\frac{1}{2}\overrightarrow{AB}$$-\frac{2}{3}\overrightarrow{AD}$(用$\overrightarrow{AB}$和$\overrightarrow{AD}$表示)
如图,在正方形ABCD中,点E是DC的中点,点F是BC的一个三等分点,那么$\overrightarrow{EF}$=$\frac{1}{2}\overrightarrow{AB}$$-\frac{2}{3}\overrightarrow{AD}$(用$\overrightarrow{AB}$和$\overrightarrow{AD}$表示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
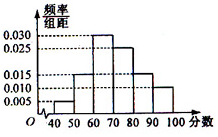 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )| A. | 588 | B. | 480 | C. | 450 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 图象关于点$({-\frac{π}{6},0})$中心对称 | B. | 图象关于$x=-\frac{π}{6}$轴对称 | ||
| C. | 在区间$[{-\frac{5π}{12},-\frac{π}{6}}]$单调递增 | D. | 在$[{-\frac{π}{12},\frac{5π}{12}}]$单调递增 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com