
已知椭圆E: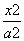 +
+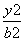 =1(a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且
=1(a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且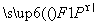 ·
·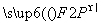 =-6.
=-6.
(1)求椭圆E的方程;
(2)若M,N是直线x=5上的两个动点,且F1M⊥F2N,则以MN为直径的圆C是否过定点?请说明理由.
(1)设点F1,F2的坐标分别为(-c,0),(c,0)(c>0),则 =(3+c,1),
=(3+c,1),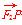 =(3-c,1),
=(3-c,1),
故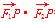 =(3+c)(3-c)+1=10-c2=-6,可得c=4,所以2a=|PF1|+|PF2|=
=(3+c)(3-c)+1=10-c2=-6,可得c=4,所以2a=|PF1|+|PF2|= =6
=6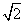 ,
,
故a=3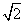 ,b2=a2-c2=18-16=2,
,b2=a2-c2=18-16=2,
所以椭圆E的方程为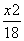 +
+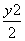 =1.
=1.
(2)设M,N的坐标分别为(5,m),(5 ,n),则
,n),则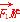 =(9,m),
=(9,m),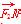 =(1,n),又
=(1,n),又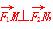 可得
可得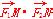 =9+mn=0,即mn=-9,又圆C的圆心为
=9+mn=0,即mn=-9,又圆C的圆心为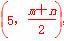 ,半径为
,半径为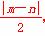 ,故圆C的方程为(x-5)2+
,故圆C的方程为(x-5)2+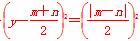
即(x-5)2+y2-(m+n)y+mn=0,
也就是(x-5)2+y2-(m+n)y-9=0,
令y=0,可得x=8或2,
故圆C必过定点(8,0)和(2,0).


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
已知曲线C的方程是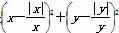 =8,给出下列三个结论:
=8,给出下列三个结论:
①曲线C与两坐标轴有公共点;
②曲线C既是中心对称图形,又是轴对称图形;
③若点P,Q在曲线C上,则|PQ|的最大值是6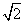 .
.
其中,所有正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
设集合A={(x,y)|(x-4)2+y2=1},B={(x,y)|(x-t)2+(y-at+2)2=1},如果命题“∃t∈R,A∩B≠∅”是真命题,则实数a的取值范围是________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合A={3,a2},集合B={0,b,1-a},且A∩B={1},则A∪B=( )
A.{0,1,3} B.{1,2,4}
C .{0,1,2,3} D.{0,1,2,3,4}
.{0,1,2,3} D.{0,1,2,3,4}
查看答案和解析>>
科目:高中数学 来源: 题型:
命题“所有实数的平方都是 正数”的否定为( )
正数”的否定为( )
A.所有实数的平方都不是正数
B.有的实数的平方是正数
C.至少有一个实数的平方是正数
D.至少有一个实数的平方不是正数
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,单摆从某点开始来回摆动,离开平衡位置O的距离s(单位:cm)和时间t(单位:s)的函数关系式为s=6sin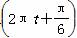 ,那么单摆来回摆动一次所需的时间为( )
,那么单摆来回摆动一次所需的时间为( )
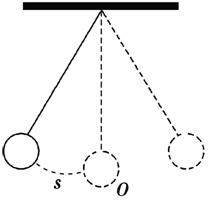
A.2πs B.πs C.0.5 s D.1 s
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com