
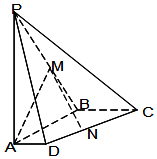
 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB的中点.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB的中点.分析 (1)以点A为原点建立如图所示的空间直角坐标系,求出$\overrightarrow{AM}$的坐标,再求出平面平面PCD的一个法向量$\overrightarrow{n}$,由$\overrightarrow{AM}•\overrightarrow{n}$=0且AM?面PCD内得答案;
(2)利用空间向量求出使直线MN与平面PAB所成的角最大时N的位置,然后再求出平面PBN的一个法向量,而$\overrightarrow{AP}$是平面PAB的一个法向量,由两个法向量所成角的余弦值求得结论.
解答 (1)证明:以A为坐标原点,建立如图所示的空间直角坐标系,则A(0 ,0,0),B(0,2,0),C(2,2,0),D(1,0,0),P(0,0,2),M(0,1,1)$\overrightarrow{AM}=(0,1,1),\overrightarrow{PD}=(1,0,-2),\overrightarrow{CD}=(-1,-2,0)$
,0,0),B(0,2,0),C(2,2,0),D(1,0,0),P(0,0,2),M(0,1,1)$\overrightarrow{AM}=(0,1,1),\overrightarrow{PD}=(1,0,-2),\overrightarrow{CD}=(-1,-2,0)$
设平面PCD的法向量是$\overrightarrow n=(x,y,z)$$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{PD}=0}\\{\overrightarrow n•\overrightarrow{CD}=0}\end{array}}\right.得\left\{{\begin{array}{l}{x-2z=0}\\{-x-2y=0}\end{array}}\right.令x=2得\overrightarrow n=(2,-1,1)$…(3分)$\overrightarrow{AM}•\overrightarrow n=0\overrightarrow{得AM}⊥\overrightarrow n$…(4分)
又$\begin{array}{l}AM?平面PCD\\∴AM∥平面PCD\end{array}$…(5分)
(2)解:由点N是线段CD上的一点,可设$\begin{array}{l}\overrightarrow{DN}=λ\overrightarrow{DC}=(λ,2λ,0),λ∈[0,1]\\ \overrightarrow{AN}=\overrightarrow{AD}+\overrightarrow{DN}=(1+λ,2λ,0)\\ \overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}=(1+λ,2λ-1,-1)\end{array}$…(7分)
平面PAB的一个法向量为$\overrightarrow{AD}=(1,0,0)$
设MN与平面PAB成θ角,则$sinθ=|cos\left?{\overrightarrow{MN},\overrightarrow{AB}}\right>|=|\frac{1+λ}{{\sqrt{5{λ^2}-2λ+3}}}|$…(8分)
令1+λ=t∈[1,2]$sinθ=\frac{t}{{\sqrt{5{{(t-1)}^2}-2(t-1)+3}}}=\frac{1}{{\sqrt{5-\frac{12}{t}+\frac{10}{t^2}}}}=\frac{1}{{\sqrt{10{{(\frac{1}{t}-\frac{3}{5})}^2}+\frac{7}{5}}}},t∈[1,2]$
当$\frac{1}{t}=\frac{3}{5}即t=\frac{5}{3}时{(sinθ)_{max}}=\frac{{\sqrt{35}}}{7},此时λ=\frac{2}{3}$…(11分)
∴当点N是线段CD上靠近点C的三等分点时,MN与平面PAB所成角最大,最大角的正弦值为$\frac{\sqrt{35}}{7}$.…(12分)
点评 本题考查了运用空间向量求证线面的垂直关系,考查了利用空间向量求解二面角的平面角,关键是建立正确的空间直角坐标系,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2n-1 | B. | -3n+2 | C. | (-1)n+1(3n-2) | D. | (-1)n+13n-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | -7 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com