
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 32 |
| 2 |
| 33 |
| 2 |
| 3n |
| 2 |
| 3 |
| 2 |
| 3k |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 9 |
| 2 |
| 32 |
| 2 |
| 33 |
| 2 |
| 3n |
| 2 |
| 3 |
| 2 |
| 3k |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| ||||
1-
|
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3k+1 |
| 2 |
| 3n |


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.
如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 2-x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| lnx |
| f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
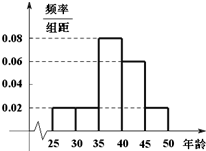 某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.
某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 25 | a | b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com