Question

在三棱柱ABC-A₁B₁C₁中，侧面ABB₁A₁为矩形，AB=1，AA₁=

2

，D为AA₁中点，BD与AB₁交于点O，CO丄侧面ABB₁A₁．
（Ⅰ）证明：BC丄AB₁；
（Ⅱ）若OC=OA，求二面角C₁-BD-C的余弦值．

Answer 1

考点：二面角的平面角及求法,直线与平面垂直的性质

专题：空间位置关系与距离,空间角

分析：（Ⅰ）由已知得tan∠AB₁B=

AB

BB1

=

2

2

，∠AB₁B=∠ABD，∠BOA=90°，由此能证明BC⊥AB₁．
（Ⅱ）连结CB₁交C₁B于E，连结OE，由已知得BD⊥OC，又BD⊥AB₁，BD⊥平面COB₁，从而∠EOC是二面角C₁-BD-C的平面角，由此能求出二面角C₁-BD-C的余弦值．

解答： （Ⅰ）证明：∵ABB₁A₁是矩形，D为AA₁的中点，
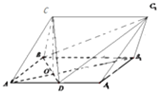
AB=1，AA₁=

2

，AD=

2

2

，
∴Rt△ABB₁中，tan∠AB₁B=

AB

BB1

=

2

2

，
∴∠AB₁B=∠ABD，
又∠BAB₁+∠AB₁B=90°，∠BAB₁+∠ABD=90°，
∴在直角三角形ABO中，∠BOA=90°，
∴BD⊥AB₁，
∴AB₁⊥面BCD，BC?面BCD，
∴BC⊥AB₁．
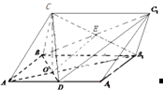
（Ⅱ）解：连结CB₁交C₁B于E，连结OE，
∵CO⊥侧面ABB₁A₁，∴BD⊥OC，又BD⊥AB₁，
∴BD⊥平面COB₁，∴BD⊥OE，
∴∠EOC是二面角C₁-BD-C的平面角，
∴BD=

6

2

，AB₁=

3

，

AD

BB1

=

AO

BB1

=

AO

OB1

=

1

2

，
OB1=

2

3

AB1=

2

3

3

，
OC=OA=

1

3

AB1=

3

3

，
在Rt△COB₁中，
B1C=

OC2+OB12

=

1 3 + 4 3

=

15

3

，
又∠EOC=∠OCE，∴cos∠EOC=

OC

CB1

=

5

5

，
∴二面角C₁-BD-C的余弦值为

5

5

．

点评：本题考查异面直线垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．