分析:(1)当a=1时,求出函数解析式,得到原函数的导函数,求得f′(2)=1,然后利用直线方程的点斜式得答案;
(2)求出a=1时导函数的零点,由零点对函数的定义域分段,求出得到区间,得到函数f(x)在x=1处取得极小值,根据函数f(x)在(0,+∞)只有唯一的极小值点求得极小值,把f(x)≥m
2-5m恒成立转化为
f(x)min≥m2-5m,解不等式求得m的取值范围;
(3)求出原函数的导函数
f′(x)=+a-=,令g(x)=ax
2+x-(a+1),然后对a进行分类讨论分析g(x)的符号,从而得到f′(x)的符号,进一步得到函数f(x)的单调区间.
解答:
解:(1)当a=1时,
f(x)=lnx+x++3,x∈(0,+∞),
∴
f′(x)=+1-=,x∈(0,+∞),
∴f′(2)=1,
即曲线y=f(x)在点(2,f(2))处的切线的斜率为1,
又f(2)=6+ln2,
故曲线y=f(x)在点(2,f(2))处的切线方程为:x-y+ln2+4=0;
(2)当a=1时,∴
f′(x)=+1-=,x∈(0,+∞),
令f′(x)=0,得:x
2+x-2=0,解得:x
1=-2(舍),x
2=1.
当x∈(0,1)时,f′(x)<0,此时函数f(x)单调递减;
当x∈(1,+∞)时,f′(x)>0,此时函数f(x)单调递增.
因此函数f(x)在x=1处取得极小值,又因为函数f(x)在(0,+∞)只有唯一的极小值点.
故函数f(x)在x=1处取得最小值f(x)
min=f(1)=6.
f(x)≥m
2-5m恒成立?
f(x)min≥m2-5m,
即:m
2-5m≤6,解得:-1≤m≤6.
故所求m的取值范围是:-1≤m≤6;
(3)∵
f′(x)=+a-=,x∈(0,+∞),
令g(x)=ax
2+x-(a+1),x∈(0,+∞),
当a=0时,g(x)=x-1,x∈(0,+∞),
此时,当x∈(0,1)时,g(x)<0,f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞)时,g(x)>0,f′(x)>0,函数f(x)单调递增.
当a≠0时,由f′(x)=0,即ax
2+x-(a+1)=0,解得:
x1=1,x2=--1.
①当
a=-时,x
1=x
2,g(x)≤0恒成立,
此时f′(x)≤0,函数f(x)在(0,+∞)递减;
②当
-<a<1时,
--1>1>0,
此时,当x∈(0,1)时,g(x)<0,f′(x)<0,函数f(x)单调递减;
当
x∈(1,--1)时,g(x)>0,f′(x)>0,函数f(x)单调递增;
当
x∈(--1,+∞)时,g(x)<0,f′(x)<0,函数f(x)单调递减.
当a>0时,
--1<0,
此时:当x∈(0,1)时,g(x)<0,f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞)时,g(x)>0,f′(x)>0,函数f(x)单调递增.
综上所述:
当a≥0时,函数f(x)在(0,1)上单调递减,
函数f(x)在(1,+∞)上单调递增;
当a=-
时,函数f(x)在(0,+∞)单调递减;
当
-<a<0时,函数f(x)在(0,1)上单调递减,
函数f(x)在
(1,--1)上单调递增,
函数f(x)在
(--1,+∞)上单调递减.



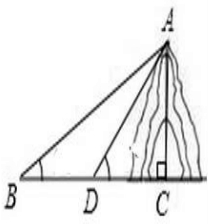 如图,从B处看山顶A的仰角为45°,向前100米,在D处看山顶A的仰角为60°,求:山AC的高度(已知sin15°=
如图,从B处看山顶A的仰角为45°,向前100米,在D处看山顶A的仰角为60°,求:山AC的高度(已知sin15°= 已知椭圆C1的中心在坐标原点,焦点在x轴上,且经过点P(
已知椭圆C1的中心在坐标原点,焦点在x轴上,且经过点P( 如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.