Question

20．为选拔参加“全市高中数学竞赛”的选手，某中学举行了一次“数学竞赛”活动．为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在[50，60），[90，100]的数据）．
（1）求样本容量n和频率分布直方图中的x、y的值并求出抽取学生的平均分；
（2）在选取的样本中，从竞赛成绩在80分以上（含80分）的学生中随机抽取2名学生参加“全市高中数学竞赛”，求所抽取的2名学生中至少有一人得分在[90，100]内的概率．

Answer 1

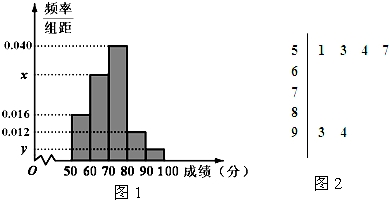
分析 （1）利用频率分布直方图能求出样本容量n和频率分布直方图中的x、y的值并求出抽取学生的平均分．
（2）由频率分布直方图得分数在[80，90）内的学生有3人，记为A，B，C，分数在[90，100]内的学生有2人，记为a，b，由此利用列举法能求出所抽取的2名学生中至少有一人得分在[90，100]内的概率．

解答 解：（1）由题意知：
样本容量n=$\frac{4}{0.016×10}$=25，y=$\frac{2}{24×10}=0.008$，
x=0.100-0.008-0.012-0.016-0.040=0.024．
由频率分布直方图得抽取的部分学生的平均分为：
55×0.16+65×0.24+75×0.4+85×0.12+95×0.08=72.2分．
（2）由频率分布直方图得分数在[80，90）内的学生有：25×0.012×10=3人，记为A，B，C，
分数在[90，100]内的学生有2人，记为a，b，
在选取的样本中，从竞赛成绩在80分以上（含80分）的学生中随机抽取2名学生参加“全市高中数学竞赛”，
基本事件总数有10个，分别为：
AB，AC，Aa，Ab，BC，Ba，Bb，Ca，Cb，ab，
所抽取的2名学生中至少有一人得分在[90，100]内包含的基本事件有7个，分别为：
Aa，Ab，Ba，Bb，Ca，Cb，ab，
∴所抽取的2名学生中至少有一人得分在[90，100]内的概率p=$\frac{7}{10}$．

点评 本题考查频率分布直方图的应用，考查概率的求法，考查频率分布直方图、概率、列举法等基础知识，考查数据处理能力、运算求解能力，考查数形结合思想，函数与方程思想，是基础题．