
定义:已知函数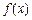 在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数
在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数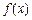 在[m,n] (m<n)上具有“DK”性质.
在[m,n] (m<n)上具有“DK”性质.
(1)判断函数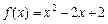 在[1,2]上是否具有“DK”性质,说明理由;
在[1,2]上是否具有“DK”性质,说明理由;
(2)若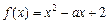 在[a,a+1]上具有“DK”性质,求a的取值范围.
在[a,a+1]上具有“DK”性质,求a的取值范围.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:解答题
设函数f(x)=x2+x-.
(1)若函数的定义域为[0,3],求f(x)的值域;
(2)若定义域为[a,a+1]时,f(x)的值域是[-,],求a的值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知y=f(x)满足f(n-1)=f(n)-lg an-1(n≥2,n∈N)且f(1)=-lg a,是否存在实数α,β,使f(n)=(αn2+βn-1)·lg a对任何n∈N*都成立,证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米 。设
。设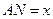 (单位:米),若
(单位:米),若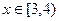 (单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
(单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。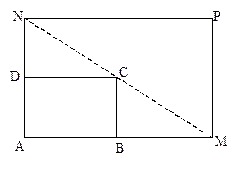
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分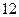 分)
分)
在股票市场上,投资者常参考 股价(每一股的价格)的某条平滑均线(记作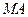 )的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的
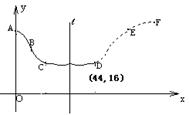
)的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的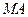 均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系
均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系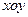 ,则股价
,则股价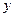 (元)和时间
(元)和时间 的关系在
的关系在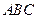 段可近似地用解析式
段可近似地用解析式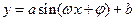 (
(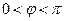 )来描述,从
)来描述,从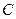 点走到今天的
点走到今天的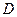 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且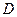 点和
点和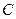 点正好关于直线
点正好关于直线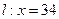 对称.老张预计这只股票未来的走势如图中虚线所示,这里
对称.老张预计这只股票未来的走势如图中虚线所示,这里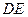 段与
段与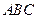 段关于直线
段关于直线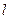 对称,
对称, 段是股价延续
段是股价延续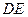 段的趋势(规律)走到这波上升行情的最高点
段的趋势(规律)走到这波上升行情的最高点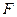 .
.
现在老张决定取点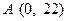 ,点
,点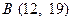 ,点
,点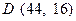 来确定解析式中的常数
来确定解析式中的常数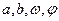 ,并且已经求得
,并且已经求得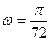 .
.
(Ⅰ)请你帮老张算出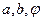 ,并回答股价什么时候见顶(即求
,并回答股价什么时候见顶(即求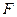 点的横坐标).
点的横坐标).
(Ⅱ)老张如能在今天以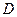 点处的价格买入该股票
点处的价格买入该股票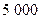 股,到见顶处
股,到见顶处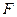 点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com