
| 销售时间x(月) | 1 | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
分析 计算$\overline{x}$、$\overline{y}$,求出回归系数$\stackrel{∧}{b}$、$\stackrel{∧}{a}$,写出回归直线方程;根据线性回归方程计算x=6时$\stackrel{∧}{y}$的值即可.
解答 解:由已知数据可得$\overline{x}$=$\frac{1+2+3+4+5}{5}$=3,
$\overline{y}$=$\frac{0.4+0.5+0.6+0.6+0.4}{5}$=0.5,
所以$\sum_{i=1}^{5}$ (xi-$\overline{x}$)(yi-$\overline{y}$)=(-2)×(-0.1)+(-1)×0+0×0.1+1×0.1+2×(-0.1)=0.1,
$\sum_{i=1}^{5}$ (xi-$\overline{x}$)2=(-2)2+(-1)2+02+12+22=10,
于是回归系数为$\stackrel{∧}{b}$=$\frac{0.1}{10}$=0.01,
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=0.5-0.01×3=0.47,
∴回归直线方程为$\stackrel{∧}{y}$=0.01x+0.47;
令x=6,得$\stackrel{∧}{y}$=0.01×6+0.47=0.53,
即该商品6月份的销售额约为0.53万元.
点评 本题考查了回归直线方程的求法与应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
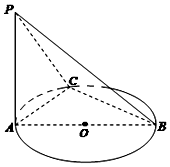 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{4}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
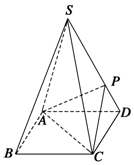 如图,四棱锥S-ABCD的底面是正方形,边长为$\sqrt{2}$,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.
如图,四棱锥S-ABCD的底面是正方形,边长为$\sqrt{2}$,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com