
分析 (1)利用x=ρcosθ,y=ρsinθ,即可得出曲线C的直角坐标方程;根据直线的斜率和点的坐标,求出直线的方程即可;
(2)设出A,B的坐标,根据弦长公式求出|AB|的长即可.
解答 解:(1)x=ρcosθ,y=ρsinθ,
由ρsin2θ-cosθ=0得ρ2sin2θ=ρcosθ.
∴y2=x即为曲线C的直角坐标方程;
点M的直角坐标为(0,1),
直线l的斜率是-1,故直线l的方程是:y-1=-x,
即x+y-1=0;
(2)设A(x1,y1),B(x2,y2)
由(1)得$\left\{\begin{array}{l}{{y}^{2}=x}\\{x+y-1=0}\end{array}\right.$,
得x2-3x+1=0,
故x1+x2=3,x1x2=1,
由弦长公式得|AB|=$\sqrt{1{+k}^{2}}$$\sqrt{{{(x}_{1}{+x}_{2})}^{2}-{{4x}_{1}x}_{2}}$=$\sqrt{10}$.
点评 本题考查了极坐标方程化为直角坐标方程、直线参数方程的应用、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(1,+∞) | B. | (-∞,0)∪[1,+∞) | C. | (-∞,0]∪[1,+∞) | D. | (-∞,0)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | -4 | C. | $-\frac{4}{3}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | D2+E2-4F>0,且F<0 | B. | D<0,F>0 | ||
| C. | D≠0,F≠0 | D. | F<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
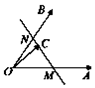 如图所示,两个非共线向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),则x2+y2的最小值为$\frac{1}{8}$.
如图所示,两个非共线向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),则x2+y2的最小值为$\frac{1}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com