
已知 ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)若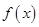 是增函数,求实数
是增函数,求实数 的取值范围;
的取值范围;
(2)当 时,求函数
时,求函数 上的最小值;
上的最小值;
(3)求证: .
.
(1)实数 的取值范围是
的取值范围是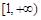 .
.
(2)当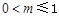 时,
时,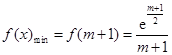 ;
;
当 时,
时,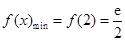 ;
;
当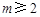 时,
时,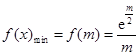 .
.
(3)见解析.
解析试题分析:(1)由题意知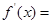
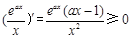 在
在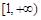 上恒成立.
上恒成立.
根据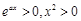 ,知
,知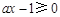 在
在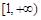 上恒成立,即
上恒成立,即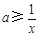 在
在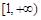 上恒成立. 只需求
上恒成立. 只需求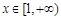 时,
时,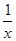 的最大值.
的最大值.
(2)当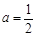 时,则
时,则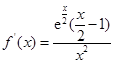 .
.
根据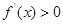 ,
,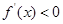 分别得到
分别得到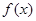 的增区间为(2,+∞),减区间为(-∞,0),(0,2). 因为
的增区间为(2,+∞),减区间为(-∞,0),(0,2). 因为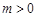 ,所以
,所以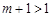 ,
,
因此,要讨论①当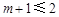 ,即
,即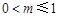 时,②当
时,②当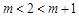 ,即
,即 时,③当
时,③当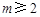 时等三种情况下函数的最小值.
时等三种情况下函数的最小值.
(3)由(2)可知,当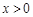 时,
时,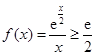 ,从而
,从而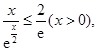
可得 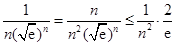 ,
,
故利用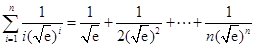
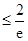
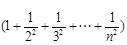
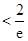
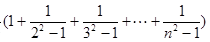
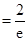
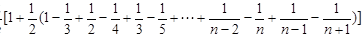
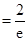
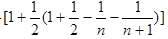
(1)由题意知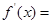
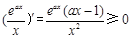 在
在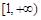 上恒成立.
上恒成立.
又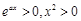 ,则
,则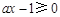 在
在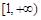 上恒成立,
上恒成立,
即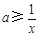 在
在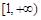 上恒成立. 而当
上恒成立. 而当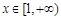 时,
时,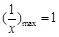 ,所以
,所以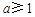 ,
,
于是实数 的取值范围是
的取值范围是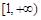 . 4分
. 4分
(2)当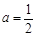 时,则
时,则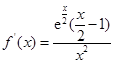 .
.
当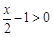 ,即
,即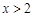 时,
时,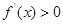 ;
;
当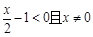 ,即
,即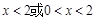 时,
时,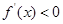 .
.
则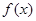 的增区间为(2,+∞),减区间为(-∞,0),(0,2). 6分
的增区间为(2,+∞),减区间为(-∞,0),(0,2). 6分
因为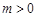 ,所以
,所以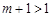 ,
,
①当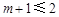 ,即
,即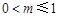 时,
时,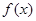 在[
在[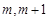 ]上单调递减,
]上单调递减,
所以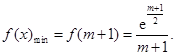
②当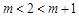 ,即
,即 时,
时,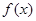 在
在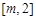 上单调递减,
上单调递减,
在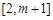 上单调递增,所以
上单调递增,所以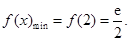


科目:高中数学 来源: 题型:解答题
水库的蓄水量随时间而变化,现用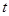 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于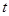 的近似函数关系式为
的近似函数关系式为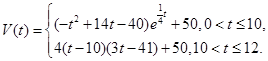
(1)该水库的蓄求量小于50的时期称为枯水期.以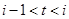 表示第1月份(
表示第1月份(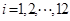 ),同一年内哪几个月份是枯水期?
),同一年内哪几个月份是枯水期?
(2)求一年内该水库的最大蓄水量(取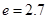 计算).
计算).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ln x-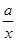 .
.
(1)当a>0时,判断f(x)在定义域上的单调性;
(2)f(x)在[1,e]上的最小值为 ,求实数a的值;
,求实数a的值;
(3)试求实数a的取值范围,使得在区间(1,+∞)上函数y=x2的图象恒在函数y=f(x)图象的上方.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=ex-ax-2.
(1)求f(x)的单调区间;
(2)若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数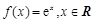 .
.
(1)求f(x)的反函数的图象上图象上,点(1,0)处的切线方程;
(2)证明: 曲线y =" f" (x)与曲线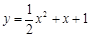 有唯一公共点.
有唯一公共点.
(3)设a<b, 比较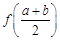 与
与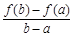 的大小, 并说明理由.
的大小, 并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com