
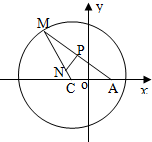
 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在线段AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.求曲线E的方程.
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在线段AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.求曲线E的方程. 分析 通过向量关系,判断点N的轨迹为曲线E.满足椭圆定义,然后求解椭圆的方程即可.
解答 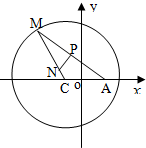 解:$\overrightarrow{AM}=2\overrightarrow{AP}$,$\overrightarrow{NP}•\overrightarrow{AM}=0$,
解:$\overrightarrow{AM}=2\overrightarrow{AP}$,$\overrightarrow{NP}•\overrightarrow{AM}=0$,
所以NP为线段AM的垂直平分线,|NA|=|NM|,
$|{NC}|+|{NA}|=|{NC}|+|{NM}|=2\sqrt{2}>2=|{CA}|$,
所以动点N的轨迹是以C(-1,0),A(1,0)为焦点的椭圆,…..(3分)
且长轴长为$2a=2\sqrt{2}$,焦距2c=2,所以$a=\sqrt{2}$,c=1,b2=1,
曲线E的方程为$\frac{x^2}{2}+{y^2}=1$.….(6分)
点评 本题考查椭圆的定义的应用,轨迹方程的求法,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,5,9,10} | B. | {1,5,9} | C. | {2,4,6} | D. | {2,4,6,8} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{80}{3}$ | B. | $\frac{255}{4}$ | C. | $\frac{624}{5}$ | D. | $\frac{1295}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com