
分析 (1)利用等差数列的定义及其通项公式即可得出.
(2)根据等比数列的前n项和公式即可求出.
解答 解:(1)设等差数列{log3(a1-1)}(n∈N*)的公差为d,
由S7=28,得log3(a4-1)=4; …(2分)
又a2=10,即log3(a2-1)=2,…(3分)
则$d=\frac{{{{log}_3}({a_4}-1)-{{log}_3}({a_2}-1)}}{2}=1$,…(5分)
所以log3(an-1)=2+(n-2)×1=n,…(6分)
故${a_n}={3^n}+1$.…(7分)
(2)由(1)知${b_n}=\frac{1}{{({3^{n+1}}+1)-({3^n}+1)}}=\frac{1}{2}•\frac{1}{3^n}$…(9分)
所以,Tn=b1+b2+b3+…+bn=$\frac{1}{2}(\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+…\frac{1}{3^n})$…(10分)
=$\frac{1}{2}×\frac{{\frac{1}{3}×(1-\frac{1}{3^n})}}{{1-\frac{1}{3}}}$=$\frac{1}{4}-\frac{1}{{4•{3^n}}}$…(12分)
点评 本题主要考查数列的通项公式和数列求和,要求熟练掌握等差数列和等比数列的通项公式和求和公式,考查学生的运算能力.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 20、8 | B. | 24、10 | C. | 10.5、24.5 | D. | 24.5、10.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
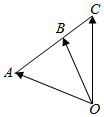 如图,$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$的终点A、B、C在一条直线上,且$\overrightarrow{AC}$=-3$\overrightarrow{CB}$,则以下等式成立的是( )
如图,$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$的终点A、B、C在一条直线上,且$\overrightarrow{AC}$=-3$\overrightarrow{CB}$,则以下等式成立的是( )| A. | $\overrightarrow{OC}$=-$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{3}{2}$$\overrightarrow{OB}$ | B. | $\overrightarrow{OC}$=-$\overrightarrow{OA}$+2$\overrightarrow{OB}$ | C. | $\overrightarrow{OC}$=$\frac{3}{2}$$\overrightarrow{OA}$-$\frac{1}{2}$$\overrightarrow{OB}$ | D. | $\overrightarrow{OC}$=$\overrightarrow{OA}$-2$\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
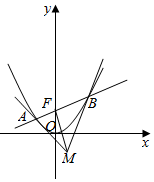 如图,已知F是抛物线x2=2py(p>0)的焦点,O为坐标原点,过点O、F的圆的圆心为Q,点Q到抛物线准线的距离为$\frac{3}{2}$.过点F的直线l交抛物线于A,B两点,过A,B分别作抛物线的切线,两切线交点为M.
如图,已知F是抛物线x2=2py(p>0)的焦点,O为坐标原点,过点O、F的圆的圆心为Q,点Q到抛物线准线的距离为$\frac{3}{2}$.过点F的直线l交抛物线于A,B两点,过A,B分别作抛物线的切线,两切线交点为M.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i<6?,1000 | B. | i<7?,1500 | C. | i<8?,1850 | D. | i<9?,2050 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com