
分析 由已知可求sinx>0,利用同角三角函数基本关系式可求sinx,进而可求cosx,利用二倍角公式可求sin2x,cos2x的值,根据两角和的正弦函数公式可求sin(2x+$\frac{π}{4}$)的值.
解答 解:∵sinx-cosx=$\frac{1}{5}$,sin2x+cos2x=1,
∴可得:25sin2x-5sinx-12=0,解得:sinx=$\frac{4}{5}$或-$\frac{3}{5}$,
又∵0≤x≤π,sinx≥0,
∴sinx=$\frac{4}{5}$,
∴cosx=sinx-$\frac{1}{5}$=$\frac{3}{5}$,sin2x=2sinxcosx=$\frac{24}{25}$,cos2x=2cos2x-1=-$\frac{7}{25}$,
∴sin(2x+$\frac{π}{4}$)=sin2xcos$\frac{π}{4}$+cos2xsin$\frac{π}{4}$=$\frac{24}{25}×\frac{\sqrt{2}}{2}$-$\frac{7}{25}×\frac{\sqrt{2}}{2}$=$\frac{17\sqrt{2}}{50}$.
故答案为:$\frac{17\sqrt{2}}{50}$.
点评 本题主要考查了同角三角函数基本关系式,二倍角公式,两角和的正弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:选择题
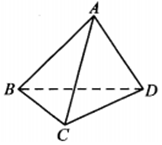 在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )
在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )| A. | θ的最大值为60° | B. | θ的最小值为60° | C. | θ的最大值为30° | D. | θ的最小值为30° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{23}{4}$ | B. | $\frac{23}{4}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,2) | B. | (3,5) | C. | (5,3) | D. | (8,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com