
 如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是
如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线.若其中经过点M、N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是| 以A为圆心的圆的半径 | 以B为圆心的圆的半径 | |
| M | 3 | 10 |
| N | 5 | 7 |
| P | 7 | 3 |
| Q | 3 | 8 |
| 13 |
| 2 |
| 5 | ||
|
| 10 |
| 13 |
| 5 |
| 6 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 | ||
|


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
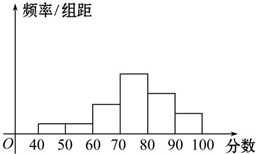 从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.估计这次数学竞赛成绩的平均数
从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.估计这次数学竞赛成绩的平均数查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com