
分析 (Ⅰ)根据正弦定理化简已知的式子求出sinC,再由锐角三角形的特征求出角C的大小;
(Ⅱ)根据余弦定理和条件可得7=a2+b2-ab,利用三角形的面积公式和条件求出ab和a2+b2的值,由完全平方公式即可求出a+b的值.
解答 解:(Ⅰ)由题意知,$\frac{a}{sinA}=\frac{2c}{\sqrt{3}}$,
根据正弦定理得,$\frac{a}{sinA}=\frac{c}{sinC}=\frac{2c}{\sqrt{3}}$,则sinC=$\frac{\sqrt{3}}{2}$,
∵△ABC是锐角三角形,∴C=$\frac{π}{3}$;
(Ⅱ)由余弦定理得,c2=a2+b2-2abcosC,
则7=a2+b2-ab,即ab=a2+b2-7,①
∵△ABC的面积为$\frac{3\sqrt{3}}{2}$,∴$\frac{3\sqrt{3}}{2}$=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{4}$ab,
解得ab=6,代入①可得a2+b2=13,
∴(a+b)2=a2+b2+2ab=25,则a+b=5.
点评 本题考查了正弦、余弦定理,三角形的面积公式,以及整体代换的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
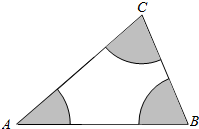 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2 | D. | $\frac{1+\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
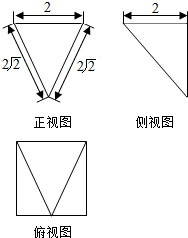
| A. | $\frac{4\sqrt{6}}{3}$ | B. | 2$\sqrt{6}$ | C. | $\frac{4\sqrt{7}}{3}$ | D. | 4$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OC=4,OB=3.
如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OC=4,OB=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
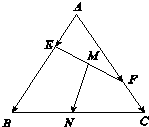 如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )
如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com