【题目】在平面直角坐标系xOy中，设命题p：椭圆C： + =1的焦点在x轴上；命题q：直线l：x﹣y+m=0与圆O：x2+y2=9有公共点． 若命题p、命题q中有且只有一个为真命题，求实数m的取值范围．

参考答案：

【答案】解：命题p为真：由题意得，m＞8﹣m＞0，解得4＜m＜8．
命题q为真：x﹣y+m=0与圆O：x2+y2=9有公共点
则圆心O到直线l的距离：d= ≤3，
解得：﹣3 ≤m≤3 ．
因为命题p、命题q中有且只有一个为真命题
若p真q假，则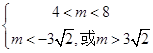： 解得：3 ＜m＜8．
若p假q真，则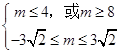： 解得：﹣3 ≤m≤4
综上：实数m的取值范围是3 ＜m＜8或﹣3 ≤m≤4．
【解析】求出命题p，q为真时，m的范围，结合命题p、命题q中有且只有一个为真命题，分类讨论，综合后可得实数m的取值范围．
【考点精析】认真审题，首先需要了解命题的真假判断与应用(两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系)．

关闭