
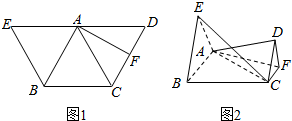
 如图1,已知正三角形ABC,以AB、AC为边在同一平面内向外作正三角形ABE与ACD,F为CD中点,分别沿AB、AF将平面ABE、平面ADE折成直二面角,连接EC、CD,如图2所示.
如图1,已知正三角形ABC,以AB、AC为边在同一平面内向外作正三角形ABE与ACD,F为CD中点,分别沿AB、AF将平面ABE、平面ADE折成直二面角,连接EC、CD,如图2所示.分析 (1)根据面面平行的性质定理证明平面DEF∥平面ABE,即可证明CD∥平面ABE;
(2)建立空间坐标系,利用向量法即可求二面角E-AC-B的余弦值.
解答 (1)证明:取AB的中点O,连接EO,OC,则EO⊥AB,0C⊥AB,
∵平面ABE⊥平面ABC,
∴EO⊥平面ABC,
∵平面ADE⊥平面ABC,F为CD中点,
∴DF⊥AF,DF⊥CF,
则DF⊥平面ABC,
则DF∥OE,则DF∥平面ABE,
∵CF∥AB,∴则CF∥平面ABE,
∵DF∩CF=F,
∴平面DEF∥平面ABE,
∵CD?平面CDF
∴CD∥平面ABE;
(2)以O为原点,以OA,0C,0E为x,y,z轴建立空间直角坐标系,
设OB=1,
则B(1,0,0),C(0,$\sqrt{3}$,0),A(-1,0,0),E(0,0,$\sqrt{3}$),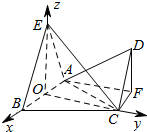
则$\overrightarrow{AC}$=(1,$\sqrt{3}$,0),$\overrightarrow{AE}$=(1,0,$\sqrt{3}$)
则平面ABC的法向量为$\overrightarrow{n}$=(0,0,1),
设平面EAC的法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AC}=0}\\{\overrightarrow{m}•\overrightarrow{AE}=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{x+\sqrt{3}y=0}\\{x+\sqrt{3}z=0}\end{array}\right.$,令x=$\sqrt{3}$,则y=-1,z=-1,即$\overrightarrow{m}$=($\sqrt{3}$,-1,-1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-1}{\sqrt{3+1+1}}=\frac{-1}{\sqrt{5}}$=-$\frac{\sqrt{5}}{5}$
由于二面角E-AC-B是锐二面角,
∴二面角E-AC-B的余弦值是$\frac{\sqrt{5}}{5}$.
点评 本题综合考查空间中线线、线面的位置关系和空间中角的计算,涉及二面角的平面角,传统方法和坐标向量法均可,考查的知识面较广,难度中等.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 150° | C. | 30°或150° | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
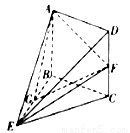
如图,在几何体 中,四边形
中,四边形 是正方形,正三角形
是正方形,正三角形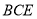 的边长为2,
的边长为2,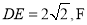 为线段
为线段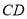 上一点,
上一点,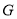 为线段
为线段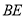 的中点.
的中点.
(1)求证:平面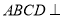 平面
平面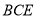 ;
;
(2)求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
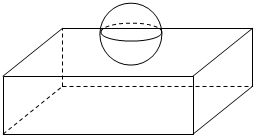 “80后文艺膏年小张在”祭我们逝去的青春“系列活动中,设计了一个与弹珠有关的玩具模型,它是由一个长方体和一个球焊接而成,如图所示,该几何体的球半径为R,其长方体的长和宽都是6R,高为$\frac{3}{2}$R:
“80后文艺膏年小张在”祭我们逝去的青春“系列活动中,设计了一个与弹珠有关的玩具模型,它是由一个长方体和一个球焊接而成,如图所示,该几何体的球半径为R,其长方体的长和宽都是6R,高为$\frac{3}{2}$R:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
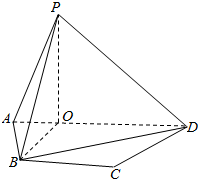 如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.
如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com