练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知数列{an}首项为1，且满足an+1=
    n+1
    n
    an，那么an等于（　　）
    A、n
    B、n+1
    C、
    n+1
    n
    D、
    n
    n+1
    考点：数列递推式
    专题：点列、递归数列与数学归纳法
    分析：根据数列之间的关系，利用累积法即可得到结论．
    解答： 解：∵an+1=
    n+1
    n
    an，
    ∴
    an+1
    an
    =
    n+1
    n
    ，
    则
    a2
    a1
    =
    2
    1
    ，
    a3
    a2
    =
    3
    2
    …
    an
    an-1
    =
    n
    n-1
    ，
    两边同时相乘得
    a2
    a1
    •
    a3
    a2
    …
    an
    an-1
    =
    2
    1
    •
    3
    2
    …
    n
    n-1
    ，
    即
    an
    a1
    =n    ，
    即an=na1=n，
    故选：A．
    点评：本题主要考查数列通项公式的求解，利用累积法是解决本题的关键，比较基础．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    对于数列{an}（n∈N*，an∈N*），若bk为a1，a2，a3，…，ak中的最大值，则称数列{bn}为数列{an}的“凸值数列”．如数列2，1，3，7，5的“凸值数列”为2，2，3，7，7．由此定义可知，自然数列1，2，3，…，n，…的“凸值数列”的通项公式bn=
     
    ；“凸值数列”为1，3，3，9，9的所有数列{an}的个数为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    根据如图的流程图，则输出的结果是（　　）
    A、7B、8C、720D、5040

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列选项中，p是q的必要不充分条件的是（　　）
    A、p：f（x）=x3+2x2+mx+1在R上单调递增；q：m≥
    4
    3
    B、p：x=1；q：x=x2
    C、p：a+bi（a，b∈R）是纯虚数；q：a=0
    D、p：a+c＞b+d；q：a＞b且c＞d

    查看答案和解析>>

    科目：高中数学 来源： 题型：

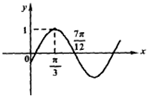    已知导函数f′（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
    π
    2
    ）的部分图象如图所示，且f（0）=-
    		3
    4
    ，则y=f（x）的图象可由函数g（x）=
    1
    2
    cosx的图象（纵坐标不变）（　　）
    A、先把各点的横坐标缩短到原来的
    1
    2
    倍，再向右平移
    5π
    12
    个单位
    B、先把各点的横坐标伸长到原来的2倍，再向右平移
    5π
    6
    个单位
    C、先把各点的横坐标缩短到原来的
    1
    2
    倍，再向左平移
    5π
    12
    个单位
    D、先把各点的横坐标伸长到原来的2倍，再向左平移
    5π
    6
    个单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知关于x的方程sin2x+cosx+a=0有解，则a的取值范围是（　　）
    A、[-1，1]
    B、[-1，
    5
    4
    ]
    C、[-
    5
    4
    ，1]
    D、[-
    5
    4
    ，-1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

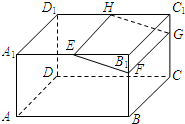    如图，在长方体ABCD-A1B1C1D1中，E，H分别是棱A1B1，D1C1上的点（点E与B1不重合），且EH∥A1D1，过EH的平面与棱BB1，CC1相交，交点分别为F，G．设AB=2AA1=2a．在长方体ABCD-A1B1C1D1内随机选取一点，记该点取自于几何体A1ABFE-D1DCGH内的概率为P，当点E，F分别在棱A1B1，BB1上运动且满足EF=a时，则P的最小值为（　　）
    A、
    11
    16
    B、
    3
    4
    C、
    13
    16
    D、
    7
    8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在一次独立性检验中，得出2×2列联表如下：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)

    A
    .
    A
    		 合计
    B 200 800 1000
    .
    B
    		 180 a 180+a
    合计 380 800+a 1180+a
    且最后发现，两个分类变量A和B没有任何关系，则a的可能值是（　　）
    A、200B、720
    C、100D、180

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    △ABC中，a、b、c分别是角A、B、C的对边，已知b2+c2=a2+bc，
    AC
    •
    AB
    =4，求S△ABC．

    查看答案和解析>>

    同步练习册答案