
分析 (1)设等差数列{an}的首项为a1,公差为d,由已知列方程组求得首项和公差,代入等差数列的通项公式求得答案;
(2)把(1)中求得的{an}的通项公式代入2${\;}^{{a}_{n}-1}$=λTn-2,得到Tn,分类求出{cn}的通项公式,由首项不适合n≥2时的通项公式,可得{cn}不是等比数列.
解答 解:(1)设等差数列{an}的首项为a1,公差为d,
由a5+a6=24,S11=143,
得$\left\{\begin{array}{l}{2{a}_{1}+9d=24}\\{11({a}_{1}+5d)=143}\end{array}\right.$,解得a1=3,d=2.
∴an=3+2(n-1)=2n+1;
(2)由2${\;}^{{a}_{n}-1}$=λTn-2,且an=2n+1,
得22n=λTn-2,
∴${T}_{n}=\frac{{2}^{2n}+2}{λ}$,
则${c}_{1}={T}_{1}=\frac{6}{λ}$;
当n≥2时,${c}_{n}={T}_{n}-{T}_{n-1}=\frac{{2}^{2n}+2-{2}^{2n-2}-2}{λ}$=$\frac{3•{2}^{2n-2}}{λ}$.
验证${c}_{1}=\frac{3}{λ}$不适合上式,
∴数列{cn}不是等比数列.
点评 本题考查等差数列的通项公式,考查了等差数列的前n项和,训练了由数列的前n项和求数列的通项公式,是中档题.


科目:高中数学 来源: 题型:解答题
 如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,BD=$\sqrt{3}$,PD⊥平面ABCD.
如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,BD=$\sqrt{3}$,PD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
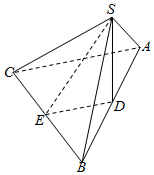 如图,在三棱锥S-ABC中,SD⊥平面ABC,D为AB的中点,E为BC的中点,AC=BC.
如图,在三棱锥S-ABC中,SD⊥平面ABC,D为AB的中点,E为BC的中点,AC=BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-x-2=0,则x=2”的逆否命题为“x≠2,则x2-x-2≠0” | |
| B. | 若命题p:?x∈R,x2+x+1=0,则¬p:?x∈R,x2+x+1≠0 | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | “x>2”是“x2-3x+2>0”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是真命题,¬p:?x∈(0,$\frac{π}{2}}$),sinx≥x | B. | p是真命题,¬p:?x0∈(0,$\frac{π}{2}}$),sinx0≥x0 | ||
| C. | p是假命题,¬p:?x∈(0,$\frac{π}{2}}$),sinx≥x | D. | p是假命题,¬p:?x0∈(0,$\frac{π}{2}}$),sinx0≥x0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com