
分析 (1)求出函数的导数,求出切线的斜率,运用两点的斜率公式,计算化简即可得到a=2;
(2)函数f (x)不能在x=1处取得极值.求出导数,讨论x>1,0<x<1函数的单调性,即可得到结论;
(3)当1<x<2时,$\frac{2}{x-1}$>$\frac{1}{lnx}$-$\frac{1}{ln(2-x)}$.运用函数的单调性和不等式的性质,即可得到结论.
解答 解:(1)f′(x)=lnx+$\frac{1}{x}$+1-a,
依题设得 $\frac{f(e)-(2-e)}{e-0}$=f′(e),即
e+1-a(e-1)-(2-e)=e$({1+\frac{1}{e}+1-a})$,
解得a=2;
(2)函数f (x)不能在x=1处取得极值.
因为f′(x)=lnx+$\frac{1}{x}$-1,记g(x)=ln x+$\frac{1}{x}$-1,则g′(x)=$\frac{x-1}{{x}^{2}}$.
①当x>1时,g′(x)>0,所以g(x)在(1,+∞)是增函数,
所以g(x)>g(1)=0,所以f′(x)>0;
②当0<x<1时,g′(x)<0,所以g(x)在(0,1)是减函数,
所以g(x)>g(1)=0,即有f′(x)>0.
由①②得f (x)在(0,+∞)上是增函数,
所以x=1不是函数f (x)极值点.
(3)当1<x<2时,$\frac{2}{x-1}$>$\frac{1}{lnx}$-$\frac{1}{ln(2-x)}$.
证明如下:由(2)得f (x)在(1,+∞)为增函数,
所以当x>1时,f(x)>f (1)=0.
即(x+1)lnx>2(x-1),所以 $\frac{1}{lnx}$<$\frac{x+1}{2(x-1)}$.①
因为1<x<2,所以0<2-x<1,$\frac{1}{2-x}$>1,所以$\frac{1}{ln\frac{1}{2-x}}$<$\frac{\frac{1}{2-x}+1}{2(\frac{1}{2-x}-1)}$=$\frac{3-x}{2(x-1)}$,
即-$\frac{1}{ln(2-x)}$<$\frac{3-x}{2(x-1)}$.②
①+②得 $\frac{1}{lnx}$-$\frac{1}{ln(2-x)}$<$\frac{x+1}{2(x-1)}$+$\frac{3-x}{2(x-1)}$=$\frac{2}{x-1}$.
点评 本题考查导数的运用:求切线的斜率和极值,同时考查不等式的大小比较,注意运用单调性和不等式的性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{27}{2}$ | B. | 6 | C. | $\frac{9}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 0 | D. | 与m的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
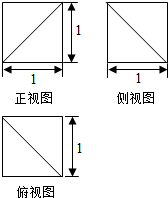 某几何体的三视图如图所示,则该几何体的体积是( )
某几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为梯形,PD⊥底面ABCD,AB∥CD,AD⊥CD,AD=AB=1,BC=$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为梯形,PD⊥底面ABCD,AB∥CD,AD⊥CD,AD=AB=1,BC=$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com