Question

18．杨辉是中国南宋末年的一位杰出的数学家、教育家，杨辉三角是杨辉的一大重要研究成果，它的许多性质与组合数的性质有关，杨辉三角中蕴藏了许多优美的规律．在杨辉三角中，第0行的数1记为C₀⁰，第n行从左到右的n+1个数分别记为C_n⁰，C_n¹，C_n²，…，C_nⁱ，…，C_nⁿ．如图是一个11阶杨辉三角：
（1）求第15行中从左到右的第3个数；
（2）试探究在杨辉三角形的某一行能否出现三个连续的数，使它们的比是3：4：5，并 证明你的结论；
（3）在第3斜列中，前5个数依次为1，3，6，10，15；第4斜列中，第5个数为35，我们发现1+3+6+10+15=35，事实上，一般地有这样的结论：第m斜列中（从右上到左下）前k个数之和，一定等于第m+1斜列中第k个数．试用含有m，k（m，k∈N^*）的数学式子表示上述结论，并证明．

Answer 1

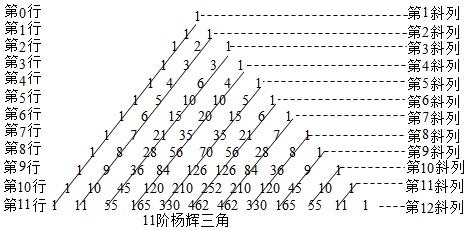
分析 （1）根据数阵中数的排列规律，可得第n行的从左到右第m+1个数为C_n^m，（n∈N，m∈N且m≤n），由此即可算出第15行中从左到右的第3个数的大小；
（2）假设在杨辉三角形的某一行能出现三个连续的数，使它们的比是3：4：5，由此列两个关于n和r的方程组，能够解出对应的n和r的值，说明假设成立；
（3）根据题意，所求结论可表示为C_m-1^m-1+C_m^m-1+…+C_m+k-2^m-1=C_m+k-1^m（m、k∈N^*且k≤m）．再由组合数的性质：C_m^m+C_m^m-1=C_m+1^m，代入等式的左边进行化简整理，即可得到该等式成

解答 解：（1）由题意，得第n行的从左到右第m+1个数C_n^m，（n∈N，m∈N且m≤n），
∴第15行中从左到右的第3个数C₁₅²=105；
（2）假设在杨辉三角形的一行能出现三个相邻的数，使得它们的比为3：4：5，
则不妨设这三个数为C_n^r-1，C_n^r，C_n^r+1
∴C_n^r-1：C_n^r：C_n^r+1=3：4：5
解得r=27，n=62
故在杨辉三角形的第62行出现三个相邻的数，使得它们的比为3：4：5．．
（3）用公式表示为：C_m-1^m-1+C_m^m-1+…+C_m+k-2^m-1=C_m+k-1^m（m、k∈N^*且k≤m）
证明：左式=C_m-1^m-1+C_m^m-1+…+C_m+k-2^m-1
=C_m^m+C_m^m-1+…+C_m+k-2^m-1=C_m+1^m+C_m+1^m-1+…+C_m+k-2^m-1
=…=C_m+k-2^m+C_m+k-2^m-1=C_m+k-1^m=右式
即等式C_m-1^m-1+C_m^m-1+…+C_m+k-2^m-1=C_m+k-1^m（m、k∈N^*且k≤m）成立．

点评 本题给出三角形数阵，求它的指定项和在m斜列中包含的等式．着重考查了组合数的性质、运用组合数解决实际应用问题、方程与恒等式的处理与证明等知识，属于中档题