
在某医学实验中,某实验小组为了分析某药物用药量与血液中某种抗体水平的关系,选取六只实验动物进行血检,得到如下资料:
| 动物编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 用药量x(单位) | 1 | 3 | 4 | 5 | 6 | 8 |
| 抗体指标y(单位) | 3.4 | 3.7 | 3.8 | 4.0 | 4.2 | 4.3 |
记s为抗体指标标准差,若抗体指标落在(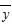 -s,
-s,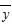 +s)内,则称该动物为有效动物,否则称为无效动物.研究方案规定先从六只动物中选取两只,用剩下的四只动物的数据求线性回归方程,再对被选取的两只动物数据进行检验.
+s)内,则称该动物为有效动物,否则称为无效动物.研究方案规定先从六只动物中选取两只,用剩下的四只动物的数据求线性回归方程,再对被选取的两只动物数据进行检验.
(1)求选取的两只动物都是有效动物的概率;
(2)若选取的是编号为1和6的两只动物,且利用剩余四只动物的数据求出y关于x的线性回归方程为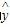 =0.17x+a,试求出a的值;
=0.17x+a,试求出a的值;
(3)若根据回归方程估计出的1号和6号动物抗体指标数据与检验结果误差都不超过抗体指标标准差,则认为得到的线性回归方程是可靠的.试判断(2)中所得线性回归方程是否可靠.
参考公式:样本数据x1,x2,…,xn的标准差:
S=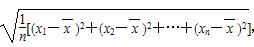 ,其中
,其中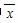 为样本平均数.
为样本平均数.
(1) 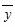 =3.9,s≈0.31.故1、6号为无效动物,2、3、4、5号为有效动物.
=3.9,s≈0.31.故1、6号为无效动物,2、3、4、5号为有效动物.
记从六只动物中选取两只为事件A.
所有可能结果为(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共15种.
满足题意的有(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共6种.故P(A)=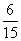 =
=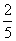 .
.
(2)对于2、3、4、5号动物,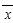 =4.5,
=4.5,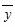 =3.925,
=3.925,
代入 =0.17x+a得a=3.16.
=0.17x+a得a=3.16.
(3)由 =0.17x+3.16得
=0.17x+3.16得 1=3.33,
1=3.33, 6=4.52.
6=4.52.
误差e1=0.07,e6=0.22,均比标准差s≈0.31小,故(2)中回归方程可靠.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
某工厂对一批产品进行了抽样检测,下图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品个数是( )
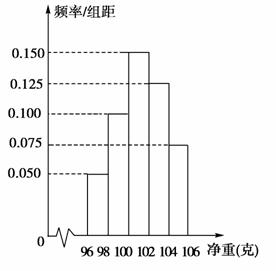
A.90 B.75
C.60 D.45
查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程为 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性相关系数r和相关指数R2都是描述线性相关强度的量,r和R2越大,相关强度越强.
④在一个2×2列联表中,计算得χ2=13.079,则有99%的把握确认这两个变量间有关系.
其中错误的个数是( )
A.0 B.1
C.2 D.3
本题可以参考独立性检验临界值表:
| P(χ2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P(χ2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
由数据(x1,y1),(x2,y2),…,(x10,y10)求得线性回归方程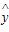 =
=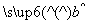 x+
x+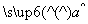 ,则“(x0,y0)满足线性回归方程
,则“(x0,y0)满足线性回归方程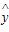 =
=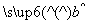 x+
x+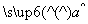 ”是
”是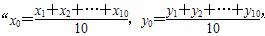 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机调查了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
| 月收入 (单位:百元) | [15, 25) | [25, 35) | [35, 45) | [45, 55) | [55, 65) | [65, 75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上统计数据填下面2×2列联表,并回答是否有99%的把握认为“月收入以5500为分界点对‘楼市限购令’的态度有差异”;
|
| 月收入不低于55 百元的人数 | 月收入低于55 百元的人数 | 合计 |
| 赞成 | a= | c= | |
| 不赞成 | b= | d= | |
| 合计 |
(2)若对月收入在[15,25),[25,35)的被调查人中各随机选取1人进行追踪调查,求选中的2人中不赞成“楼市限购令”人数至多1人的概率.
| P(χ2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
K2=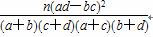
查看答案和解析>>
科目:高中数学 来源: 题型:
一个袋子中装有六个大小形状完全相同的小球,其中一个编号为1,两个编号为2,三个编号为3.现从中任取一球,记下编号后放回,再任取一球,则两次取出的球的编号之和等于4的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某单位有7个连在一起的车位,现有3辆不同型号的车需停放,如果要求剩余的4个车位连在一起,则不同的停放方法的种数为( )
A.16 B.18
C.24 D.32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com