
分析 (Ⅰ)由椭圆定义得:|F2Q|=|F2P|+|PQ|=|F2P|+|PF1|=2a,点Q的轨迹是以F2为圆心,2a为半径的圆,当QF2⊥F1F2时△QF1F2面积最大,推出ac=2,结合离心率,然后求解椭圆方程即可.
(Ⅱ)联立$\left\{\begin{array}{l}y=kx+m\\ \frac{y^2}{4}+\frac{x^2}{3}=1\end{array}\right.$通过△=0,推出${k^2}=\frac{{{m^2}-4}}{3}$求出m≥2,设圆心F2(0,-1)到直线MN的距离为d,求出弦长,设点F1(0,1)到直线MN的距离为h,求出三角形的面积的表达式,然后求解范围即可.
解答 解:(Ⅰ)由椭圆定义得:|F2Q|=|F2P|+|PQ|=|F2P|+|PF1|=2a,
所以点Q的轨迹是以F2为圆心,2a为半径的圆.(1分)
当QF2⊥F1F2时△QF1F2面积最大,所以$\frac{1}{2}•2c•2a=4$得:ac=2(2分)
又$\frac{c}{a}=\frac{1}{2}$可得a=2,c=1. (3分)
所以Q点轨迹E的方程x2+(y+1)2=16,椭圆C的方程$\frac{y^2}{4}+\frac{x^2}{3}=1$(5分)
(Ⅱ)由$\left\{\begin{array}{l}y=kx+m\\ \frac{y^2}{4}+\frac{x^2}{3}=1\end{array}\right.$得(3k2+4)x2+6kmx+3m2-12=0△=36k2m2-4(3k2+4)(3m2-12)=0
化简得:3k2-m2+4=0(7分)
所以,${k^2}=\frac{{{m^2}-4}}{3}$
由${k^2}=\frac{{{m^2}-4}}{3}≥0$及m>0得,m≥2
(8分)
设圆心F2(0,-1)到直线MN的距离为d,则$d=\frac{|m+1|}{{\sqrt{1+{k^2}}}}=\sqrt{\frac{3(m+1)}{m-1}}$
所以,弦长 $|MN|=2\sqrt{16-{d^2}}=2\sqrt{\frac{13m-19}{m-1}}$(9分)
设点F1(0,1)到直线MN的距离为h,则$h=\frac{|m-1|}{{\sqrt{1+{k^2}}}}=\sqrt{\frac{3(m-1)}{m+1}}$(10分)
所以,${S_{△{F_{\;}}_1MN}}=\frac{1}{2}|MN|•h=\sqrt{\frac{3(13m-19)}{m+1}}=\sqrt{39-\frac{96}{m+1}}$
由m≥2,得:$\sqrt{39-\frac{96}{m+1}}∈[\sqrt{7},\sqrt{39})$
所以,${S_{△{F_{\;}}_1MN}}$的取值范围为$[\sqrt{7},\sqrt{39})$. (12分)
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的综合应用,三角形的面积的求法,点到直线的距离公式的应用,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $2+\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $2+\sqrt{5}$ | D. | $\sqrt{5}-2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 160 | B. | 180 | C. | 200 | D. | 220 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(x)可能没有零点 | B. | g(x)可能有1个零点 | C. | g(x)可能有2个零点 | D. | g(x)可能有3个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
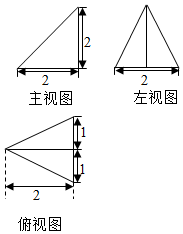 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )| A. | $\frac{4}{3}$ | B. | $\frac{4}{9}$ | C. | $\sqrt{6}-2$ | D. | $3\sqrt{6}-6$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com