
分析 (1)依题意,直线l1的方程为,利用点到直线间的距离公式可求得点C到直线l1的距离d=$\frac{丨{y}_{1}{x}_{2}-{x}_{1}{y}_{2}丨}{\sqrt{{x}_{1}^{2}+{y}_{1}^{2}}}$,再利用|AB|=2|AO|=2$\sqrt{{x}_{1}^{2}+{y}_{1}^{2}}$,可证得S=|AB|d=2|x1y2-x2y1|;当l1与l2时的斜率之一不存在时,同理可知结论成立;
(2)方法一:设直线l1的斜率为k,则直线l2的斜率为-$\frac{1}{2k}$,可得直线l1与l2的方程,联立方程组,可求得x1、x2、y1、y2,继而可求得答案.
方法二:设直线l1、l2的斜率分别为$\frac{{y}_{1}}{{x}_{1}}$、$\frac{{y}_{2}}{{x}_{2}}$,则$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,利用A(x1,y1)、C(x2,y2)在椭圆x2+2y2=1上,求得|x1y2-x2y1|=$\frac{\sqrt{2}}{2}$,可求得面积S=2|x1y2-x2y1|=$\sqrt{2}$.
解答 解:(1)依题意,直线l1的方程为y=$\frac{{y}_{1}}{{x}_{1}}$x,
由点到直线间的距离公式得:点C到直线l1的距离d=$\frac{丨\frac{{y}_{1}{x}_{2}}{{x}_{1}}-{y}_{2}丨}{\sqrt{1+(\frac{{y}_{1}}{{x}_{1}})^{2}}}$=$\frac{丨{y}_{1}{x}_{2}-{x}_{1}{y}_{2}丨}{\sqrt{{x}_{1}^{2}+{y}_{1}^{2}}}$,
由|AB|=2|AO|=2$\sqrt{{x}_{1}^{2}+{y}_{1}^{2}}$,
∴S=|AB|d=2|x1y2-x2y1|;
当l1与l2时的斜率之一不存在时,同理可知结论成立;
(2)方法一:设直线l1的斜率为k,则直线l2的斜率为-$\frac{1}{2k}$,
设直线l1的方程为y=kx,联立方程组$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+2{y}^{2}=1}\end{array}\right.$,消去y解得x=±$\frac{1}{\sqrt{1+2{k}^{2}}}$,
根据对称性,设x1=$\frac{1}{\sqrt{1+2{k}^{2}}}$,则y1=$\frac{k}{\sqrt{1+2{k}^{2}}}$,
同理可得x2=$\frac{\sqrt{2}k}{\sqrt{1+2{k}^{2}}}$,y2=$\frac{-\frac{\sqrt{2}}{2}}{\sqrt{1+2{k}^{2}}}$,
∴S=2|x1y2-x2y1|=$\sqrt{2}$.
方法二:设直线l1、l2的斜率分别为$\frac{{y}_{1}}{{x}_{1}}$、$\frac{{y}_{2}}{{x}_{2}}$,则$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,
∴x1x2=-2y1y2,
∴x12x22=4y12y22=-2x1x2y1y2,
∵A(x1,y1)、C(x2,y2)在椭圆x2+2y2=1上,
∴(x12+2y12)(x22+2y22)=x12x22+4y12y22+2(x12y22+x22y12)=1
即-4x1x2y1y2+2(x12y22+x22y12)=1,
∴(x1y2-x2y1)2=$\frac{1}{2}$,即|x1y2-x2y1|=$\frac{\sqrt{2}}{2}$,
∴S=2|x1y2-x2y1|=$\sqrt{2}$.
点评 本题考查直线与圆锥曲线的综合应用,考查方程思想、等价转化思想与综合运算能力,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 菱形 | C. | 梯形 | D. | 矩形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 四棱锥P-ABCD中,底面ABCD是矩形,∠PCD=90°,二面角P-CD-B为60°,BC=1,AB=PC=2.
四棱锥P-ABCD中,底面ABCD是矩形,∠PCD=90°,二面角P-CD-B为60°,BC=1,AB=PC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
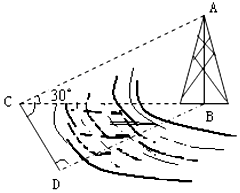 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{3}{2},5}]$ | B. | $[{\frac{2}{3},5}]$ | C. | $[{\frac{3}{2},7}]$ | D. | $[{\frac{2}{3},7}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com