
设数列{an}的前n项和为Sn,并且满足2Sn=a +n,an>0(n∈N*).
+n,an>0(n∈N*).
(1)猜想{an}的通项公式,并用数学归纳法加以证明.
(2)设x>0,y>0,且x+y=1,证明: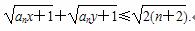
(1)分别令n=1,2,3,
得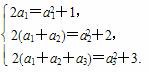
∵an>0,∴a1=1,a2=2,a3=3.
猜想:an=n.
由2Sn=a +n.①
+n.①
可知,当n≥2时,2Sn-1=a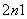 +(n-1).②
+(n-1).②
①-②,得2an=a -a
-a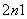 +1,
+1,
即a =2an+a
=2an+a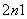 -1.
-1.
(ⅰ)当n=2时,a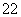 =2a2+12-1,
=2a2+12-1,
∵a2>0,∴a2=2.
(ⅱ)假设当n=k(k≥2)时,ak=k,那么当n=k+1时,
a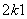 =2ak+1+a
=2ak+1+a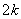 -1=2ak+1+k2-1
-1=2ak+1+k2-1
⇒[ak+1-(k+1)][ak+1+(k-1)]=0,
∵ak+1>0,k≥2,∴ak+1+(k-1)>0,
∴ak+1=k+1.
即当n=k+1时也成立.
∴an=n(n≥2).
显然n=1时,也成立,故对于一切n∈N*,均有an=n.
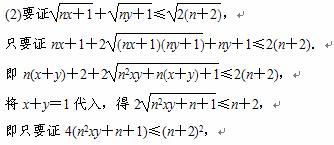 即4xy≤1.
即4xy≤1.
∵x>0,y>0,且x+y=1,∴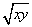 ≤
≤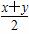 =
= ,
,
即xy≤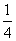 ,故4xy≤1成立,所以原不等式成立.
,故4xy≤1成立,所以原不等式成立.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
数列{an}中,已知a1=1,当n≥2时,an-an-1=2n-1,依次计算a2、a3、a4后,猜想an的表达式是( )
A.an=3n-2 B.an=n2
C.an=3n-1 D.an=4n-3
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(n)=1+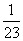 +
+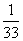 +
+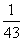 +…+
+…+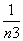 ,g(n)=
,g(n)=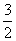 -
-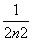 ,n∈N*.
,n∈N*.
(1)当n=1,2,3时,试比较f(n)与g(n)的大小;
(2)猜想f(n)与g(n)的大小关系,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在△ABC中,∠A=90°,正方形DEFG的边长是6cm,且四个顶点都在△ABC的各边上,CE=3 cm,则BC的长为( )
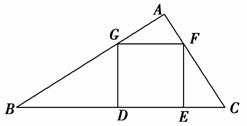
A.12cm B.21cm
C.18cm D.15cm
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆O于点A、B,C、D,弦AD和BC交于点Q,割线PEF经过点Q交圆O于点E、F,点M在EF上,且∠BAD=∠BMF.
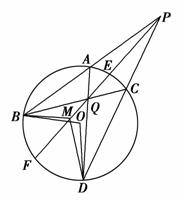
(1)求证:PA·PB=PM·PQ;
(2)求证:∠BMD=∠BOD.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合M={x||2x-1|<2},N=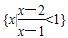 ,则M∩N等于( )
,则M∩N等于( )
A.{x|1<x<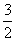 } B.{x|
} B.{x| <x<1}
<x<1}
C.{x|- <x<
<x<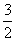 } D.{x|-
} D.{x|- <x<
<x<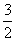 ,且x≠1}
,且x≠1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com