
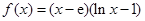
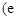 为自然对数的底数).
为自然对数的底数).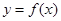 在
在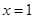 处的切线方程;
处的切线方程;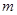 是
是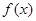 的一个极值点,且点
的一个极值点,且点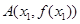 ,
,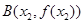 满足条件:
满足条件: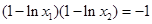 .
.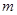 的值;
的值;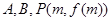 是三个不同的点, 判断
是三个不同的点, 判断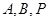 三点是否可以构成直角三
三点是否可以构成直角三 ;(2)
;(2) ;点
;点 ,
, ,
, 可构成直角三角形.
可构成直角三角形.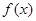 求导,将切点的横坐标1代入到
求导,将切点的横坐标1代入到 中得到切线的斜率,代入到
中得到切线的斜率,代入到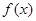 中得到切点的纵坐标,从而利用点斜式得到切线方程;第二问,先求函数的定义域,令
中得到切点的纵坐标,从而利用点斜式得到切线方程;第二问,先求函数的定义域,令 ,得到方程的根,将定义域断开,判断函数的单调性,从而求出函数极值;第三问,先排除几个特例情况,在一般情况中,要证明三角形为直角三角形,只需判断2边垂直,用向量垂直的充要条件证明即可.
,得到方程的根,将定义域断开,判断函数的单调性,从而求出函数极值;第三问,先排除几个特例情况,在一般情况中,要证明三角形为直角三角形,只需判断2边垂直,用向量垂直的充要条件证明即可. ,
,  ,又
,又 ,所以曲线
,所以曲线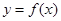 在
在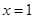 处的切线方程为
处的切线方程为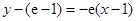 ,即
,即 .
. ,定义域为
,定义域为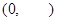 .
. 时,
时, ,
, ,∴
,∴ ;
; 时,
时,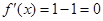 ;当
;当 时,
时,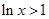 ,
, ,∴
,∴
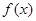 存在唯一的极值点
存在唯一的极值点 ,∴
,∴ ,则点
,则点 为
为
 ,则
,则 ,与条件
,与条件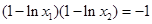 不符,
不符, .同理可得
.同理可得 .
. ,则
,则 ,与条件
,与条件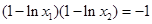 不符,从而得
不符,从而得 .
.  ,
, ,
, 两两不重合.
两两不重合.



 ,点
,点 ,
, ,
, 可构成直角三角形.
可构成直角三角形.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com