
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最小值即可;
(2)由题意可得a≥lnx-$\frac{3x}{2}$-$\frac{1}{2x}$,在(0,+∞)上恒成立,构造函数h(x)=lnx-$\frac{3x}{2}$-$\frac{1}{2x}$,h′(x)=-$\frac{(x-1)(3x+1)}{{2x}^{2}}$,求解最大值,即可求解a的取值范围.
解答 解:(1)函数f(x)的定义域是(0,+∞),
f′(x)=2lnx+2,
令f′(x)>0,解得:x>$\frac{1}{e}$
令f′(x)<0,解得:0<x<$\frac{1}{e}$,
故函数f(x)在(0,$\frac{1}{e}$)递减,在($\frac{1}{e}$,+∞)递增;
故f(x)的最小值是f($\frac{1}{e}$)=-$\frac{2}{e}$-1;
(2)不等式f(x)≤3x3+2ax恒成立,
可得:a≥lnx-$\frac{3x}{2}$-$\frac{1}{2x}$,在(0,+∞)上恒成立,
设h(x)=lnx-$\frac{3x}{2}$-$\frac{1}{2x}$,
h′(x)=$\frac{1}{x}$-$\frac{3}{2}$+$\frac{1}{{2x}^{2}}$=-$\frac{(x-1)(3x+1)}{{2x}^{2}}$,
h′(x)=0,得:x=1,x=-$\frac{1}{3}$(舍去),
当0<x<1时,h′(x)>0,
当x>1时,h′(x)<0,
∴当x=1时,h(x)max=-2,
∴a≥-2,
∴实数a的取值范围:[-2,+∞).
点评 本题考查了利用导数在函数单调性中的应用,运用导数求解函数最值,解决不等式恒成立问题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
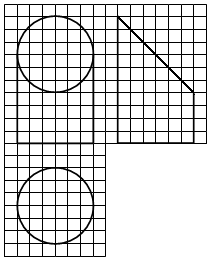 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )| A. | 90π | B. | 63π | C. | 42π | D. | 36π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com