
分析 (1)设河水速度为$\overrightarrow{{v}_{0}}$、轮渡速度为$\overrightarrow{{v}_{1}}$,轮渡实际航行的速度为$\overrightarrow{v}$,由题意能用向量表示河水速度、轮渡速度以及轮渡实际航行的速度.
(2)由$\overrightarrow{{v}_{1}}=6$km/h,$\overrightarrow{{v}_{0}}$=km/h,$\overrightarrow{v}⊥\overrightarrow{{v}_{0}}$,利用勾股定理能求出轮船航行的实际速度.
解答 解:(1)设河水速度为$\overrightarrow{{v}_{0}}$、轮渡速度为$\overrightarrow{{v}_{1}}$,轮渡实际航行的速度为$\overrightarrow{v}$,
由题意用向量表示河水速度、轮渡速度以及轮渡实际航行的速度如下图: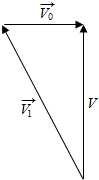
(2)∵$\overrightarrow{{v}_{1}}=6$km/h,$\overrightarrow{{v}_{0}}$=km/h,$\overrightarrow{v}⊥\overrightarrow{{v}_{0}}$,
∴轮船航行的实际速度$\overrightarrow{v}$=$\sqrt{{6}^{2}-{2}^{2}}$=$\sqrt{32}$=4$\sqrt{2}$≈5.656(km/h).
点评 本题考查向量表示河水速度、轮渡速度以及轮渡实际航行的速度,考查轮船航行的实际速度的大小的求法,是基础题,解题时要注意向量三角形法则的合理运用.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
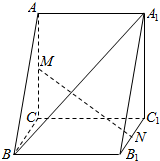 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{23}{12}$ | B. | $\frac{\sqrt{6}}{12}$ | C. | $\frac{23\sqrt{6}}{12}$ | D. | -$\frac{23\sqrt{6}}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com