
分析 根据根式,分数指数幂和对数的运算法则分别进行计算即可.
解答 解:(1)原式=$\frac{5}{3}$-($\frac{2}{3}$)${\;}^{3×\frac{1}{3}}$-1+$\sqrt{\frac{1}{4}}$=$\frac{5}{3}$-$\frac{2}{3}$-1+$\frac{1}{2}$=$\frac{1}{2}$.
(2)原式=log2$\sqrt{\frac{7}{72}}$+log26-log2$\sqrt{28}$=log2$\frac{\sqrt{\frac{7}{72}}×6}{\sqrt{28}}$=log2$\sqrt{\frac{7}{72}×36×\frac{1}{28}}$=log2$\sqrt{\frac{1}{8}}$=log2${2}^{-\frac{3}{2}}$=$-\frac{3}{2}$.
点评 本题主要考查对数和指数幂的运算,根据相应的对应法则是解决本题的关键.


科目:高中数学 来源: 题型:选择题
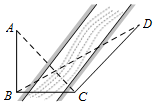 如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )
如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )| A. | 10米 | B. | $10\sqrt{2}$米 | C. | $10\sqrt{3}$米 | D. | $20\sqrt{3}$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平行四边形ABCD的两条对角线相交于点M,点N为CD的中点.若$\overrightarrow{AB}$=(4,0),$\overrightarrow{AD}=(4,4)$.
如图,平行四边形ABCD的两条对角线相交于点M,点N为CD的中点.若$\overrightarrow{AB}$=(4,0),$\overrightarrow{AD}=(4,4)$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | t≤8 | B. | t≥8 | C. | t≤9 | D. | t≥9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com