
分析 设△PF1F2的内切圆半径为r,由|PF1|-|PF2|=2a,|F1F2|=2c,用△PF1F2的边长和r表示出等式中的三角形的面积,解此等式求出λ.
解答 解:双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的a=4,b=3,c=$\sqrt{16+9}$=5,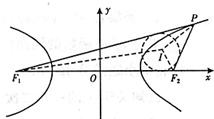
设△PF1F2的内切圆半径为r,
由双曲线的定义得|PF1|-|PF2|=2a,|F1F2|=2c,
S${\;}_{△IP{F}_{1}}$ =$\frac{1}{2}$|PF1|•r,S${\;}_{△IP{F}_{2}}$=$\frac{1}{2}$|PF2|•r,
S△${\;}_{I{F}_{1}{F}_{2}}$=$\frac{1}{2}$•2c•r=cr,
由${S_{△IP{F_1}}}={S_{△IP{F_2}}}+λ•{S_{△I{F_1}{F_2}}}$得,
$\frac{1}{2}$|PF1|•r=$\frac{1}{2}$|PF2|•r+λcr,
故λ=$\frac{|P{F}_{1}|-|P{F}_{2}|}{2c}$=$\frac{a}{c}$=$\frac{4}{5}$,
故答案为:$\frac{4}{5}$.
点评 本题考查双曲线的定义和简单性质,利用待定系数法求出参数的值是关键,考查方程思想和运算能力,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | eπ+1>π•ee | B. | 3eπ<πe3 | C. | 3e2>2e3 | D. | e${\;}^{\sqrt{2}}$<$\sqrt{2}$e |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com