
| A�� | 7 | B�� | 6 | C�� | 5 | D�� | 4 |
���� ��x��[-3��-1]ʱ��g��x��=2$\sqrt{1-��x+2��^{2}}$����x��[1��3]ʱ��g��x��=$\frac{1}{2}\sqrt{1-��x-2��^{2}}$����ͬһ����ϵ�У�����f��x����g��x����ͼ������ͼ����4�����㣬�ɵý��ۣ�
��� 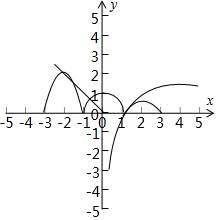 �⣺�߶�����x��R����g��x��=$\frac{1}{2}$g��x+2������x��[-1��1]ʱ��g��x��=$\sqrt{1-{x^2}}$��
�⣺�߶�����x��R����g��x��=$\frac{1}{2}$g��x+2������x��[-1��1]ʱ��g��x��=$\sqrt{1-{x^2}}$��
�൱x��[-3��-1]ʱ��g��x��=2$\sqrt{1-��x+2��^{2}}$����x��[1��3]ʱ��g��x��=$\frac{1}{2}\sqrt{1-��x-2��^{2}}$��
��ͬһ����ϵ�У�����f��x����g��x����ͼ������ͼ����4�����㣬
�ຯ��y=f��x��-g��x��������[-4��4]�����ĸ���Ϊ4��
��ѡD��
���� ���⿼�麯�������ж����������ν�ϵ���ѧ˼�룬����ѧ�������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 40 | B�� | 35 | C�� | 12 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x��R��x2��0 | B�� | $?{x_0}��R��{x_0}^2��0$ | C�� | $?{x_0}��R��{x_0}^2��0$ | D�� | $?{x_0}��R��{x_0}^2��0$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
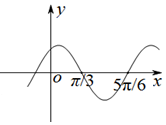 ��֪����f��x��=sin����x+�գ����أ�0��0���գ��У���ͼ����ͼ��ʾ����f��x����ͼ������ƽ��$\frac{��}{6}$����λ���õ�g��x����ͼ������g��x���Ľ���ʽΪ��������
��֪����f��x��=sin����x+�գ����أ�0��0���գ��У���ͼ����ͼ��ʾ����f��x����ͼ������ƽ��$\frac{��}{6}$����λ���õ�g��x����ͼ������g��x���Ľ���ʽΪ��������| A�� | g��x��=sin2x | B�� | g��x��=cos2x | C�� | $g��x��=sin��2x+\frac{��}{6}��$ | D�� | $g��x��=sin��2x+\frac{2��}{3}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��1�� | B�� | ��0��1] | C�� | ��1��+�ޣ� | D�� | [1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪ij�����������ͼ��ͼ��ʾ����ü���������Ϊ��������
��֪ij�����������ͼ��ͼ��ʾ����ü���������Ϊ��������| A�� | $\frac{4}{3}$+�� | B�� | 4+�� | C�� | $\frac{4}{3}$+2�� | D�� | 4+2�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com