
分析 (1)依题意,可得数列{an+1}是以2为首项,2为公比的等比数列,于是可求得数列{an}的通项公式an和Sn;
(2)化简bn=(an+1)log${\;}_{\frac{1}{2}}$(an+1)为bn=-n•2n,利用错位相减法可求得数列{bn}的前n项和为Tn=(1-n)2n+1-2,代入Tn+n•2n+1>50可得使之成立的正整数n的最小值.
解答 解:(1)∵点{an,an+1)在直线y=2x+1上,
∴an+1=2an+1,即an+1+1=2(an+1),又a1=1,a1+1=2,
∴数列{an+1}是以2为首项,2为公比的等比数列,
∴an+1=2n,
∴an=2n-1.
Sn=a1+a2+…an=(21+22+…+2n)-n=$\frac{2(1{-2}^{n})}{1-2}$-n=2n+1-n-2.
(2)∵bn=(an+1)log${\;}_{\frac{1}{2}}$(an+1)=2nlog${\;}_{\frac{1}{2}}$2n=-n•2n,
∴-Tn=1•21+2•22+…+n•2n,①
-2Tn=1•22+2•23+…+…+(n-1)•2n+n•2n+1,②
①-②得:Tn=21+22+…+2n-n•2n+1=2n+1-2-n•2n+1=(1-n)2n+1-2.
要使Tn+n•2n+1>50成立,即(1-n+n)2n+1-2=2n+1-2>50成立,
∵25=32<52,26=64>52,即当n+1≥6,n≥5时,2n+1-2>50恒成立,
∴使Tn+n•2n+1>50成立的正整数n的最小值为5.
点评 本题考查数列的递推式,考查等比数列的关系的确定与通项公式的求法,突出考查错位相减法求和的应用,考查转化思想与运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{6}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | p |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)≤2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
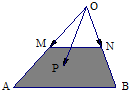 如图所示,在△OAB中,M、N分别是OA、OB的中点,点P在梯形ABNM区域(含边界)上移动,且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$,则4x+3y的取值范围是[3,8].
如图所示,在△OAB中,M、N分别是OA、OB的中点,点P在梯形ABNM区域(含边界)上移动,且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$,则4x+3y的取值范围是[3,8].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
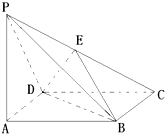 如图,四棱锥P-ABCD的底面是边长为a的正方形,PA⊥平面ABCD,PA=a,E为CP中点,
如图,四棱锥P-ABCD的底面是边长为a的正方形,PA⊥平面ABCD,PA=a,E为CP中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com