考点:命题的真假判断与应用
专题:简易逻辑
分析:由f(x)=1+3x+2x
2+4x
3+5x
4=(((5x+4)x+2)x+3)x)+1,能判断①的正误;由正弦定理能判断②的正误;由函数f(x)=cosx•sinx=
sin2x能判断③的正误;若存在正实数t
0,使得
=t
0,则|
+
|=|
|+|
|.
解答:
解:在①中,∵f(x)=1+3x+2x
2+4x
3+5x
4=(((5x+4)x+2)x+3)x)+1,
∴用秦九韶算法计算多项式f(x)=1+3x+2x
2+4x
3+5x
4在x=0.3的值时,
公进行了4次乘法和4次加法,故①正确;
在②中,在△ABC中,∵a
2tanB=b
2tanA,
∴由正弦定理
==2R,得a=2RsinA,b=2RsinB,
∴a
2tanB=b
2tanA,∴
=,∴
=,
∴sin2A=sin2B,
∴2A=2B或2A=π-2B,
∴A=B或A+B=
,∴△ABC是等腰或直角三角形,故②正确;
在③中,∵函数f(x)=cosx•sinx=
sin2x,f(x
1)=-f(x
2),
∴x
1=2kπ-x
2,k∈Z,故③错误;
在④中,若存在正实数t
0,使得
=t
0,则|
+
|=|
|+|
|,故④错误.
故选:C.
点评:本题考查命题真假的判断,涉及到秦九韶算法、三角函数、向量等知识点,是中档题.



 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案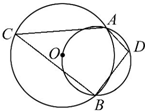 如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若∠ADB=100°,则∠ACB的度数为( )
如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若∠ADB=100°,则∠ACB的度数为( ) 如图,已知双曲线的中心在坐标原点O,左焦点为F,C是双曲线虚轴的下顶点,双曲线的一条渐近线OD与直线FC相交于点D,若双曲线的离心率为2,则∠ODF的余弦值是( )
如图,已知双曲线的中心在坐标原点O,左焦点为F,C是双曲线虚轴的下顶点,双曲线的一条渐近线OD与直线FC相交于点D,若双曲线的离心率为2,则∠ODF的余弦值是( )