
分析 (1)利用向量的模结合两角和与差的三角函数化简求解即可.
(2)利用两角和的正切函数,结合基本不等式求出最值,然后判断三角形的形状即可.
解答 解:(1)∵$|\vec a{|^2}=2{cos^2}\frac{A+B}{2}+{sin^2}\frac{A-B}{2}=\frac{3}{2}$,∴$1+cos(A+B)+\frac{1-cos(A-B)}{2}=\frac{3}{2}$;…(2分)
化简得 $cosAcosB-sinAsinB-\frac{cosAcosB+sinAsinB}{2}=0$,
所以,$\frac{1}{2}cosAcosB=\frac{3}{2}sinAsinB$,…(5分)
∴$tanAtanB=\frac{1}{3}$.…(6分)
(2)由(1)可知A,B为锐角,则tanA>0,tanB>0,…(7分)$tanC=-tan(A+B)=-\frac{tanA+tanB}{1-tanAtanB}=-\frac{3(tanA+tanB)}{2}≤-3\sqrt{tanAtanB}=-\sqrt{3}$.
(当且仅当tanA=tanB=$\frac{\sqrt{3}}{3}$,“=”成立) …(10分)
所以tanC的最大值为-$\sqrt{3}$,此时三角形的形状为等腰三角形.…(12分)
点评 本题考查三角形的解法,两角和与差的三角函数的应用,基本不等式的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥n,m∥α且n∥β,则α∥β?????????? | |
| B. | 若m⊥n,m∥α且n∥β,则α⊥β? | |
| C. | 若m∥α且n⊥m,则n⊥α???????????????????? | |
| D. | 若m⊥n,m⊥α且n⊥β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
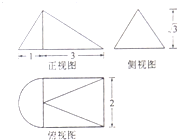
| A. | $\frac{(8+π)\sqrt{3}}{6}$ | B. | $\frac{(12+π)\sqrt{3}}{6}$ | C. | $\frac{(12+π)\sqrt{3}}{2}$ | D. | $\frac{(6+π)\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,5,9,10} | B. | {1,5,9} | C. | {2,4,6} | D. | {2,4,6,8} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com