
分析 由条件利用二次函数的性质,分类讨论求得数y=x2-4x-5在[0,a]上的最大值.
解答 解:函数y=x2-4x-5=(x-2)2-9 它的图象的对称轴方程为x=2,
当a∈(0,2)时,函数在[0,a]上单调递减,故函数的最大值为02-0-5=-5;
当a∈[2,4)时,函数在[0,2]上单调递减,在(2,a)上单调递增,故函数的最大值为02-0-5=-5;
当a≥4时,函数在[0,2]上单调递减,在(2,a]上单调递增,故函数的最大值为a2-4a-5.
故答案为:当a∈(0,4)函数的最大值为-5;a∈[4,+∞)时,函数的最大值为a2-4a-5.
点评 本题主要考查二次函数在闭区间上的最值的求法,二次函数的性质,体现了分类讨论的数学思想,属于基础题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
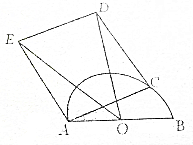 如图,线段AB长度为2,以AB为直径作半圆O,又以半圆O的一条弦AC为边作正方形ACDE,设△OED的面积为S,∠CAB=α.
如图,线段AB长度为2,以AB为直径作半圆O,又以半圆O的一条弦AC为边作正方形ACDE,设△OED的面积为S,∠CAB=α.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
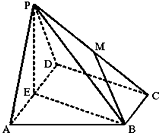 如图所示,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,PA=PD=4,BC=$\frac{1}{2}$AD=2,CD=2$\sqrt{3}$.
如图所示,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,PA=PD=4,BC=$\frac{1}{2}$AD=2,CD=2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com