
分析 根据题意,由数列{an}的前四项,归纳分析可以推测an=$\sqrt{\frac{n-1}{n+1}}$,验证n=5时是否成立,即可得答案.
解答 解:根据题意,数列{an}的前四项依次为$0,\frac{{\sqrt{3}}}{3},\frac{{\sqrt{2}}}{2},\frac{{\sqrt{15}}}{5}$,
则有a1=$\sqrt{\frac{1-1}{1+1}}$=0,
a2=$\sqrt{\frac{2-1}{2+1}}$=$\sqrt{\frac{1}{3}}$=$\frac{\sqrt{3}}{3}$,
a3=$\sqrt{\frac{3-1}{3+1}}$=$\sqrt{\frac{2}{4}}$=$\frac{\sqrt{2}}{2}$,
a4=$\sqrt{\frac{4-1}{4+1}}$=$\sqrt{\frac{3}{5}}$=$\frac{\sqrt{15}}{5}$,
则可以推测an=$\sqrt{\frac{n-1}{n+1}}$,
当n=5时,a5=$\sqrt{\frac{5-1}{5+1}}$=$\sqrt{\frac{4}{6}}$=$\frac{\sqrt{6}}{3}$,符合题意;
故答案为:$\sqrt{\frac{n-1}{n+1}}$.
点评 本题考查归纳推理的应用,关键是分析该数列的前5项,发现变化的规律.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | [15°,45°] | B. | [15°,75°] | C. | [30°,60°] | D. | [0°,90°] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2),4 | B. | (1,-2),2 | C. | (-1,2),2 | D. | (1,-2),4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(-∞,0),x3+x<0 | B. | ?x∈(-∞,0),x3+x≥0 | ||
| C. | $?{x_0}∈[0,\;+∞),\;x_0^3+{x_0}<0$ | D. | $?{x_0}∈[0,\;+∞),\;x_0^3+{x_0}≥0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数区间 | [50,70] | [70,90] | [90,110] | [110,130] | [130,150] |
| 人数 | 2 | 8 | 32 | 38 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
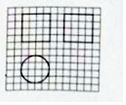 如图,网络纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三观图,切削该毛坯得到一个表面积最大的长方体,则该长方体的表面积为( )
如图,网络纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三观图,切削该毛坯得到一个表面积最大的长方体,则该长方体的表面积为( )| A. | 24 | B. | 16+32$\sqrt{2}$ | C. | 16+8$\sqrt{2}$ | D. | 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com