
 如图,在直三棱柱ABC-A1B1C1中,底面为正三角形,点M在棱BB1上,AB=4,AA1=5,
如图,在直三棱柱ABC-A1B1C1中,底面为正三角形,点M在棱BB1上,AB=4,AA1=5,分析 (1)建立空间直角坐标系,利向量法即可证明M是棱BB1的中点;
(2)求出平面的法向量.利用向量法即可求平面A1MC与平面ABC所成锐二面角的余弦值.
解答 证明:(1)取AC中点O,连OB.
在平面ACC1A1上过O作AC垂线交A1C1于N.
∵平面ACC1A1⊥平面ABC.
∴ON⊥平面ABC,
如图:以O为坐标原点,建立空间直角坐标系
由已知:A(2,0,0),B(0,2$\sqrt{3}$,0),C(-2,0,0),A1(2,0,5),B1(0,2$\sqrt{3}$,5),C1(-2,0,5),M(0,2$\sqrt{3}$,m),…(3分)
设$\overrightarrow{n}$=(x,y,z)为平面A1MC法向量
$\overrightarrow{n}•\overrightarrow{{A}_{1}C}=-4x-5z=0$,$\overrightarrow{n}•\overrightarrow{CM}=2x+2\sqrt{3}y+mz=0$,
取x=5$\sqrt{3}$,z=-4$\sqrt{3}$,y=2m-5,
即:$\overrightarrow{n}$=(5$\sqrt{3}$,2m-5,-4$\sqrt{3}$),
又$\overrightarrow{m}$=(0,1,0)为平面ACC1A1法向量
依题意:$\overrightarrow{m}•\overrightarrow{n}=2m-5=0$,解得m=$\frac{5}{2}$
∴M为棱BB1的中点 …(8分)
(2)由(1)知:$\overrightarrow{n}$=(5$\sqrt{3}$,2m-5,-4$\sqrt{3}$)为平面A1MC法向量
又$\overrightarrow{a}$=(0,0,1)为平面ABC法向量
∴cos<$\overrightarrow{a},\overrightarrow{n}$>=$\frac{-4\sqrt{3}}{\sqrt{25×3+16×3}}$=-$\frac{4\sqrt{41}}{41}$,
∴平面A1MC与平面ABC所成锐二面角余弦值为$\frac{4\sqrt{41}}{41}$.…(12分)
点评 本题主要考查空间二面角的求解,建立坐标系,利用向量法是解决线面所成角的常用方法.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 样本10,6,8,5,6的标准差是5.3 | |
| B. | “p∨q为真”是“p∧q为真”的充分不必要条件 | |
| C. | K2是用来判断两个分类变量是否相关的随机变量,当K2的值很小时可以推定两类变量不相关 | |
| D. | 设有一个回归直线方程为$\widehat{y}$=2-1.5x,则变量x毎增加一个单位,y平均减少1.5个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
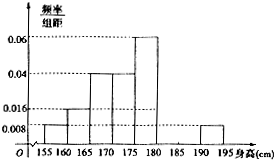 从某校的800名男生中随机抽取50人测量身高,被测学生身高介于介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…..,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某校的800名男生中随机抽取50人测量身高,被测学生身高介于介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…..,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com