
分析 (1)先求出函数的导数,通过讨论a的范围,得到函数的单调区间;
(2)分离参数得$a=\frac{{{e^x}-\frac{1}{2}{x^2}-1}}{x}$,令$g(x)=\frac{{{e^x}-\frac{1}{2}{x^2}-1}}{x}$(x∈[1,2]),通过求导得到函数g(x)的单调性,从而求出g(x)的最大值、最小值,进而求出a的范围.
解答 解:(1)f′(x)=ex-a,
当a≤0时,f′(x)≥0,则f(x)在(-∞,+∞)上单调递增,
当a>0时,f(x)在(-∞,lna)上单调递减,f(x)在(lna,+∞)上单调递增.
(2)由$F(x)=f(x)-\frac{1}{2}{x^2}=0$,得$a=\frac{{{e^x}-\frac{1}{2}{x^2}-1}}{x}$,
令$g(x)=\frac{{{e^x}-\frac{1}{2}{x^2}-1}}{x}$(x∈[1,2]),
则$g'(x)=\frac{{(x-1){e^x}-\frac{1}{2}{x^2}+1}}{x^2}$
令$h(x)=(x-1){e^x}-\frac{1}{2}{x^2}+1$,h′(x)=x(ex-1),
当1≤x≤2时,h′(x)>0,∴h(x)在[1,2]上单调递增,
∴$h(x)≥h(1)=\frac{1}{2}>0$,g′(x)>0,∴g(x)在[1,2]上单调递增,
∴$g(x)=\frac{{{e^x}-\frac{1}{2}{x^2}-1}}{x}$在[1,2]上的最小值为$g(1)=e-\frac{3}{2}$,最大值为$g(2)=\frac{1}{2}({e^2}-3)$,
∴当$e-\frac{3}{2}≤a≤\frac{1}{2}({{e^2}-3})$时,函数$F(x)=f(x)-\frac{1}{2}{x^2}$在[1,2]上有且仅有一个零点.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,(2)中分离出a,求出相关函数的单调性是解答本题的关键,本题是一道中档题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | -sin x | B. | -cos x | C. | sin x | D. | cos x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
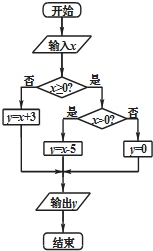 执行如图所示的程序框图,在集合A={x∈Z|-9≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间[-4,3]内的概率为( )
执行如图所示的程序框图,在集合A={x∈Z|-9≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间[-4,3]内的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{13}$ | B. | $-\frac{12}{13}$ | C. | $-\frac{13}{12}$ | D. | $\frac{13}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [1,e] | C. | [1,1+e] | D. | [e,e+1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com