
分析 (1)先求出曲线C1的普通方程,从而求出曲线C2的直角坐标方程,由此能求出曲线C2的极坐标方程.
(2)设A(ρ1,θ),$B({ρ_2},θ+\frac{π}{3})$($θ∈(-\frac{π}{2},\frac{π}{6})$),推导出|OA|+|OB|=$2\sqrt{3}cos(θ+\frac{π}{6})$,由此能求出|OA|+|OB|的取值范围.
解答 解:(1)曲线${C_1}:\left\{\begin{array}{l}x=2+2cosα\\ y=sinα\end{array}\right.$化为普通方程为:$\frac{{{{(x-2)}^2}}}{4}+{y^2}=1$,
又$\left\{\begin{array}{l}{x^'}=\frac{x}{2}\\{y^'}=y\end{array}\right.$,即$\left\{\begin{array}{l}x=2{x^'}\\ y={y^'}\end{array}\right.$代入上式可知:
曲线C2的直角坐标方程为(x-1)2+y2=1,即x2+y2=2x,
∴曲线C2的极坐标方程为ρ=2cosθ.
(2)设A(ρ1,θ),$B({ρ_2},θ+\frac{π}{3})$($θ∈(-\frac{π}{2},\frac{π}{6})$),
∴$|{OA}|+|{OB}|={ρ_1}+{ρ_2}=2cosθ+2cos(θ+\frac{π}{3})$=$2\sqrt{3}cos(θ+\frac{π}{6})$,
因为$(θ+\frac{π}{6})∈(-\frac{π}{3},\frac{π}{3})$,
所以|OA|+|OB|的取值范围是$(\sqrt{3},2\sqrt{3}]$.
点评 本题考查曲线的极坐标方程的求法,考查两线段和的取值范围的求法,考查极坐标方程、直角坐标方程、参数方程的互化,考查推理论证能力、运算求解能力,考查转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (2,0) | B. | (3,0) | C. | ($\frac{1}{2}$,-1) | D. | ($\frac{1}{3}$,-$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
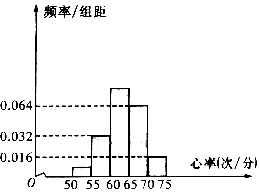 某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 心率小于60次/分 | 心率不小于60次/分 | 合计 | |
| 体育生 | 8 | 12 | 20 |
| 艺术生 | 2 | 28 | 30 |
| 合计 | 10 | 40 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份序号x | 1 | 2 | 3 | 4 | 5 |
| 录取人数y | 10 | 11 | 14 | 16 | 19 |
| 接受超常实验班教育 | 未接受超常实验班教育 | 合计 | |
| 录取少年大学生 | 60 | 20 | 80 |
| 未录取少年大学生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
| P(k2≥k0) | 0.50 | 0.40 | 0.10 | 0.05 |
| k0 | 0.455 | 0.708 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 |
| 年利润/十万元 | 1 | 6 | 15 | 28 | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com