
| ||
| 3 |
5
| ||
| 3 |
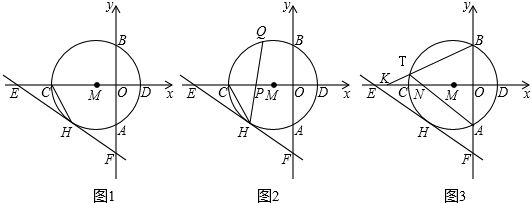
| ||
| 3 |
5
| ||
| 3 |
| ||
| 3 |
5
| ||
| 3 |
5
| ||
| 3 |
5
| ||
| 3 |
10
| ||
| 3 |
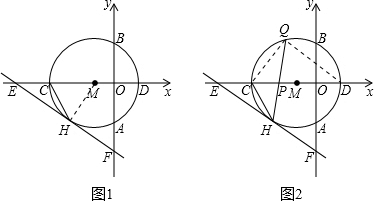
| HM |
| OF |
| EM |
| EF |
| r | ||||
|
| 4 | ||||
|
| 1 |
| 2 |
| 3 |
| 4 |
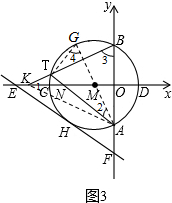
| MN |
| AM |
| AM |
| MK |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ∫ | a b |
| ∫ | b a |
| ∫ | 0 -1 |
| ∫ | 1 0 |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、若p∧(¬q)为真命题,则q为真命题 | ||||||||||
B、回归直线方程
| ||||||||||
| C、将一组数据中的每个数据都减去同一个数后,平均数与方差均没有变化 | ||||||||||
| D、某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人.为了解该单位职工的健康情况,应采用系统抽样的方法从中抽取样本 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、{1,3,4,5} |
| B、{0,2} |
| C、{0,2,3,4,5} |
| D、{1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com