Question

12．△ABC中，AB=5，AC=12，BC=13，P为△ABC平面外一点，PA=PB=PC=7
（1）求P到平面ABC的距离；
（2）求P到AC的距离；
（3）求PA，PB与平面ABC所成的角的大小．

Answer 1

分析 （1）由已知P在平面ABC上的射影是BC的中点O，由此能求出P到平面ABC的距离．
（2）过O作OD⊥AC，交AC于D，连结PD，则由三垂线定理得PD⊥AC，由此能求出P到AC的距离．
（3）由PO⊥平面ABC，得∠PAO是PA与平面ABC所成的角，∠PBO是与平面ABC所成的角，由此能求出PA，PB与平面ABC所成的角的大小．

解答 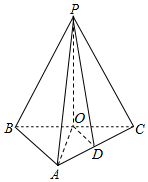解：（1）∵△ABC中，AB=5，AC=12，BC=13，
∴AB²+AC²=BC²，∴AB⊥AC，
∵PA=PB=PC=7，∴P在平面ABC上的射影是BC的中点O，
∴P到平面ABC的距离PO=$\sqrt{P{B}^{2}-B{O}^{2}}$=$\sqrt{49-\frac{169}{4}}$=$\frac{3\sqrt{3}}{2}$．
（2）过O作OD⊥AC，交AC于D，连结PD，则由三垂线定理得PD⊥AC，
∵AO=OC=$\frac{13}{2}$，∴D是AC中点，∴OD=$\sqrt{A{O}^{2}-A{D}^{2}}$=$\sqrt{\frac{169}{4}-36}$=$\frac{5}{2}$．
∴P到AC的距离PD=$\sqrt{P{O}^{2}+O{D}^{2}}$=$\sqrt{\frac{27}{4}+\frac{25}{4}}$=$\sqrt{13}$．
（3）∵PO⊥平面ABC，
∴∠PAO是PA与平面ABC所成的角，∠PBO是与平面ABC所成的角，
∵PA=PB=7，OB=OA=$\frac{13}{2}$，
∴cos∠PAO=cos∠PBO=$\frac{BO}{PB}$=$\frac{\frac{13}{2}}{7}$=$\frac{13}{14}$，
∴PA，PB与平面ABC所成的角的大小均为arccos$\frac{13}{14}$．

点评 本题考查点到平面、点到直线的距离的求法，考查线面角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．