
分析 (1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,运用等差数列和等比数列的通项公式,解方程可得公差和公比,即可得到所求;
(2)方法一、求得$\frac{{a}_{n}}{{2}^{n-1}}$=$\frac{3n-1}{{2}^{n-1}}$=$\frac{3n+2}{{2}^{n-2}}$-$\frac{3n+5}{{2}^{n-1}}$=cn-cn+1,再由裂项相消求和,化简整理即可得到所求;
方法二、三运用数列的求和方法:错位相减法和等比数列的求和公式,计算即可得到所求.
解答 解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,
由a1=b1=2,得${a_4}=2+3d,{b_4}=2{q^3},{S_4}=8+6d$,
由条件得方程组$\left\{\begin{array}{l}2+3d+2{q^3}=27\\ 8+6d-2{q^3}=10\end{array}\right.⇒\left\{\begin{array}{l}d=3\\ q=2\end{array}\right.$,
故${a_n}=3n-1,{b_n}={2^n}(n∈{N^*})$;
(2)法一:${T_n}={a_n}{b_1}+{a_{n-1}}{b_2}+{a_{n-2}}{b_3}+…+{a_1}{b_n}={2^n}{a_1}+{2^{n-1}}{a_2}+…+2{a_n}$
=${2^n}({a_1}+\frac{a_2}{2}+…+\frac{a_n}{{{2^{n-1}}}})$,
又因为$\frac{{a}_{n}}{{2}^{n-1}}$=$\frac{3n-1}{{2}^{n-1}}$=$\frac{3n+2}{{2}^{n-2}}$-$\frac{3n+5}{{2}^{n-1}}$=cn-cn+1(令${c_n}=\frac{3n+2}{{{2^{n-2}}}}$)
所以Tn=2n[(c1-c2)+(c2-c3)+…+(cn-cn+1)]=2n(c1-cn+1)
=10•2n-2(3n+5);
法二:${T_n}={a_n}{b_1}+{a_{n-1}}{b_2}+{a_{n-2}}{b_3}+…+{a_1}{b_n}={2^n}{a_1}+{2^{n-1}}{a_2}+…+2{a_n}$
=${2^n}({a_1}+\frac{a_2}{2}+…+\frac{a_n}{{{2^{n-1}}}})$,
令${M_n}={a_1}+\frac{a_2}{2}+\frac{a_3}{2^2}+…+\frac{a_n}{{{2^{n-1}}}}$,$\frac{1}{2}{M_n}=\frac{1}{2}{a_1}+\frac{a_2}{2^2}+\frac{a_3}{2^3}+…+\frac{{{a_{n-1}}}}{{{2^{n-1}}}}+\frac{a_n}{2^n}$,
两式相减得到:$\frac{1}{2}{M_n}=({{a_1}-\frac{1}{2^n}{a_n}})+3({\frac{1}{2}+\frac{1}{2^2}+…+\frac{1}{{{2^{n-1}}}}})$
=$2-\frac{3n-1}{2^n}+3•\frac{{\frac{1}{2}(1-\frac{1}{{{2^{n-1}}}})}}{{1-\frac{1}{2}}}=5-\frac{3n+5}{2^n}$,
所以${M_n}=10-\frac{3n+5}{{{2^{n-1}}}}$,
所以${T_n}={2^n}•{M_n}=10•{2^n}-2(3n+5)$.
法三:Tn=anb1+an-1b2+an-2b3+…+a2bn-1+a1bn
即${T_n}=2(3n-1)+{2^2}(3n-4)+{2^3}(3n-7)+…+{2^{n-1}}•5+{2^n}•2$,
则$2{T_n}={2^2}(3n-1)+{2^3}(3n-4)+{2^4}(3n-7)+…+{2^n}•5+{2^{n+1}}•2$,
两式相减得到:${T_n}=-2(3n-1)+3({2^2}+{2^3}+…+{2^n})+{2^{n+1}}•2$
=$-2(3n-1)+3×\frac{{4-{2^{n+1}}}}{1-2}+{2^{n+1}}×2$
=5•2n+1-6n-10=10•2n-2(3n+5).
点评 本题考查等差数列和等比数列的通项公式的运用,考查数列的求和方法:裂项相消求和和错位相减法,考查化简整理的能力,属于中档题.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (13,49) | B. | [2,2+$\sqrt{13}$] | C. | [2,13] | D. | [4,22+6$\sqrt{13}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
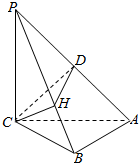 在三棱锥P-ABC中,PC⊥平面ABC,△PAC是等腰直角三角形,PA=6,AB⊥BC,CH⊥PB,垂足为H,D为PA的中点,则当△CDH的面积最大时,CB=$\sqrt{6}$.
在三棱锥P-ABC中,PC⊥平面ABC,△PAC是等腰直角三角形,PA=6,AB⊥BC,CH⊥PB,垂足为H,D为PA的中点,则当△CDH的面积最大时,CB=$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com