
分析 在①中,m与l平行或异面;在②中,由直线与平面平行的性质得α内可有无数条直线与l平行;在③中,α与β相交或平行;在④中,m与l相交、平行或异面.
解答 解:由m,n,l是直线,α,β是平面,知:
在①中:若m?α,l?β,且α∥β,则m与l平行或异面,故①错误;
在②中:若l平行于α,则由直线与平面平行的性质得α内可有无数条直线与l平行,故②正确;
在③中:若m?α,l?β,且l⊥m,则α与β相交或平行,故③错误;
在④中:若m⊥n,n⊥l,则m与l相交、平行或异面,故④错误.
故答案为:②.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x∈R,x2+x+1>0 | B. | 存在x0∈R,x02+x0+1>0 | ||
| C. | 存在x0∈R,x02+x0+1≤0 | D. | 对任意的x∈R,x2+x+1≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
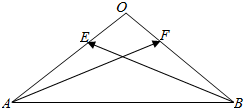 等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
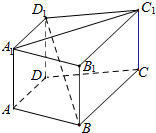 定义侧面与底面垂直的棱柱为直棱柱,在直四棱柱ABCD-A1B1C1D1中(如图),当底面四边形ABCD满足条件BD⊥AC时,有BD1⊥A1C1.
定义侧面与底面垂直的棱柱为直棱柱,在直四棱柱ABCD-A1B1C1D1中(如图),当底面四边形ABCD满足条件BD⊥AC时,有BD1⊥A1C1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|270°+k•360°<a<90°+k•360°,k∈Z} | B. | {a|-90°+k•360°<a<270°+k•360°,k∈Z} | ||
| C. | {a|-90°+k•360°<a<90°+k•360°,k∈Z} | D. | {a|-90°+k•720°<a<90°+k•720°,k∈Z} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com