
分析 (1)利用an与Sn的关系进行求数列的通项公式.
(2)由等比数列的性质可求公比q,及首项b1,即可利用等比数列的求和公式计算得解.
解答 解:(1)∵数列{an}的前n项和${S_n}={n^2},(n∈N*)$,
∴当n≥2时,${a_n}={S_n}-{S_{n-1}}={n^2}-{(n-1)^2}=2n-1$,
又当n=1时,a1=S1=3,满足上式,an=2n-1(n∈N*)
(2)由(1)可知a1=S1=3,a2=5,a3=7,又b2=S1,b4=a2+a3,
∴b2=3,b4=12.
又数列{bn}是公比为正数等比数列,
∴${q^2}=\frac{b_4}{b_2}=4$,又q>0,
∴q=2,
∴${b_1}=\frac{b_2}{q}=\frac{3}{2}$,
∴数列{bn}的前n项和${T_n}=\frac{{{b_1}(1-{q^n})}}{1-q}=\frac{{\frac{3}{2}(1-{2^n})}}{1-2}=\frac{3}{2}({2^n}-1)$.
点评 本题主要考查数列的通项公式的求法,考查了等差、等比数列的性质与求和,要求熟练掌握an与Sn的关系,考查了转化思想的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{9},\frac{1}{3})$ | B. | $(-1,-\frac{1}{3})$ | C. | $(-1,-\frac{1}{3})∪(\frac{1}{9},\frac{1}{3})$ | D. | $[{-1,-\frac{1}{3}}]∪[{\frac{1}{9},\frac{1}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{21}{8}$ | B. | 6 | C. | $\frac{21}{8}$或6 | D. | $\frac{21}{8}$或$\frac{75}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,平面PAD⊥底面ABCD.
在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,平面PAD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
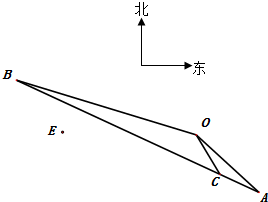 如图,某自行车手从O点出发,沿折线O-A-B-O匀速骑行,其中点A位于点O南偏东45°且与点O相距20$\sqrt{2}$千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°-α)(其中sinα=$\frac{1}{{\sqrt{26}}}$,0°<α<90°)且与点O相距5$\sqrt{13}$千米(假设所有路面及观测点都在同一水平面上).
如图,某自行车手从O点出发,沿折线O-A-B-O匀速骑行,其中点A位于点O南偏东45°且与点O相距20$\sqrt{2}$千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°-α)(其中sinα=$\frac{1}{{\sqrt{26}}}$,0°<α<90°)且与点O相距5$\sqrt{13}$千米(假设所有路面及观测点都在同一水平面上).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com